Introduction
The Lévy distribution, together with the Normal and Cauchy distribution, belongs to the class of stable distributions, and it is among the only three distributions for which the density can be derived in a closed form. The density function of the two-parameter Lévy distribution is expressed as follows: \[\begin{equation*} f(x; \lambda, \mu)=\sqrt{\dfrac{ \lambda}{2\pi}}\frac{e^{-\dfrac{ \lambda}{2(x-\mu)}}}{(x-\mu)^{\frac{3}{2}}},\;x\geq\mu,\; \lambda>0, \; \mu\in \mathbb{R}. \end{equation*}\] We specifically consider the scenario where \(\mu=0\) due to the difficulty in estimating both parameters. Despite being widely applied in various fields such as physics, biology, medicine, and finance, there exist only a limited number of specific goodness-of-fit tests for the Lévy distribution. In this blog post, we present results from [1] by introducing two new families of test statistics. Following the idea from [2] (see also references therein), the novel statistics rely on the V-empirical Laplace transform and the characterization of the Lévy distribution [3]:
Characterization 1 Suppose that \(X, Y\) and \(Z\) are independent and identically distributed random variables with density \(f\) defined on \((0, \infty)\). Then \[Z\text{ and }\dfrac{aX + bY}{\big(\sqrt{a}+\sqrt{b}\big)^2}\text{, }0 < a, b < \infty\] are identically distributed if and only if \(f\) is a density of Lévy distribution with arbitrary scale parameter \(\lambda\).
The first application of this characterization in the development of a goodness-of-fit test for the Lévy distribution was presented in [4] for the specific case of \(a=b=1\). They proposed a test statistic given by:
\(\begin{equation*} T_n^*=\int_{{\mathbb{R}^+}}\Big(\frac{1}{\binom{n}{2}}\sum\limits_{j<i}I\Big\{\frac{X_i+X_j}{4}\leq t\Big\}-F_n(t)\Big)dF_n(t). \end{equation*}\)
In [1], we extended the aforementioned statistic to cover the case of arbitrary values of \(a, b\in \mathbb{N}\). Additionally, we investigated the asymptotic distributions of these generalized test statistics.
Our test statistics
The equivalence in distribution between two random variables can also be established by equating their Laplace transforms. Considering this, our tests are constructed either as the supremum of the difference or the integrated difference of the corresponding V-empirical Laplace transforms of the terms described in the Characterization 1. The underlying rationale for this approach is that the test statistic will have small values when the sample is drawn from the Lévy distribution. The proposed test statistics are of the form:
\[\begin{align}\label{statJn} J_{n,a}&=\sup\limits_{t>0}\Big \vert \Big (\frac{1}{n^2}\sum\limits_{i, j} e^{-\frac{t(Y_{i}+Y_{j})}{4}}-\frac{1}{n}\sum\limits_{i} e^{-tY_{i}}\Big )e^{-at} t^{\frac{3}{2}}\Big \vert =\sup\limits_{t\in [0, 1]}\Big \vert \Big (\frac{1}{n^2}\sum\limits_{i, j} t^{\frac{Y_{i}+Y_{j}}{4}}-\frac{1}{n}\sum\limits_{i} t^{Y_{i}}\Big )t^{a}\big (-\log t\big)^{\frac{3}{2}}\Big \vert ,\\ R_{n, a}& =\int_{\mathbb{R}^+}\Big (\frac{1}{n}\sum\limits_{i} e^{-tY_{i}}-\frac{1}{n^2}\sum\limits_{i, j} e^{-\frac{t(Y_{i}+Y_{j})}{4}}\Big )e^{-at} t^{\frac{3}{2}}dt=\frac{3\sqrt{\pi}}{4n^2}\sum_{i, j}\Bigg(\frac{1}{\big(a+\frac{Y_i+Y_j}{4}\big)^\frac{5}{2}}-\frac{1}{2\big(a+Y_i\big)^\frac{5}{2}}-\frac{1}{2\big(a+Y_j\big)^\frac{5}{2}}\Bigg), \end{align}\] where \(Y_k=\frac{X_k}{\hat{\lambda}}\) and \(\hat{\lambda}\) is a suitably chosen estimate of \(\lambda\). We have considered maximum likelihood and median-based estimates. It should be noted that any consistent estimate of \(\lambda\) can be employed. The performance of the tests naturally varies depending on the chosen estimate.
We have determined the asymptotic distributions of the novel tests and provided the 95th percentiles of empirical distributions for large sample sizes, demonstrating a fast stabilization of the distribution. These results are summarized in the following two theorems:
Theorem 1 Let \(a\geq 1\) and \(X_1, X_2, \dots, X_n\) be i.i.d random variables distributed according to the Lévy law with scale parameter \(\lambda\). Then the following holds: \(\begin{equation*} \sqrt{n} J_{n, a}\overset{{D}}{\to} \sup\limits_{t\in [0, 1]}\mid \xi (t)\mid, \end{equation*}\) where \(\xi(t)\) is a centred Gaussian random process, having the following covariance function:
\(\begin{align} K(s,t)=& s^a t^a (-\log (s))^{3/2} (-\log (t))^{3/2} \Big(-e^{-\sqrt{2} \big(\sqrt{-\log (s)}+\sqrt{(-\log (t))}\big)}-2 e^{- \sqrt{-2(\log(s)-\frac14\log(t))}+\sqrt{-\frac{\log (t)}{2}}}\\&-2 e^{- \sqrt{2(-\log (t)-{\frac14}\log(s))}+\sqrt{-\frac{\log (s)}{2}}}+4 e^{-\frac{\sqrt{-\log (s t)}+\sqrt{-\log (s)}+\sqrt{-\log (t)}}{\sqrt{2}}}+e^{ \sqrt{-2\log (s t)}}\Big). \end{align}\)
Theorem 2 Let \(a\geq 1\) and \(X_1, X_2, \dots, X_n\) be i.i.d random variables distributed according to the Lévy law with scale parameter \(\lambda\). Then, for every \(a>0\), the asymptotic distribution of \(\sqrt{n}R_{n, a}\) as \(n\to\infty\) is normal \(\mathcal{N}(0, \sigma^2_R(a))\) where \(\sigma^2_R(a)= 4E\zeta(X; a)^2\).
The expression for \(\zeta\) is intricate, and for the exact formulation, we refer the reader to [1] for the exact expression.
Performance of novel tests
For assessing the performance of test statistics, one can usually consider their powers against a wide range of alternatives.
We conducted a power analysis of the tests at a significance level of \(\alpha=0.05\) using a Monte Carlo method with 10,000 replications (N = 10,000). The objective of our study was to compare the JEL and AJEL approaches proposed [4] with the classical approach, as well as to determine the empirical power of the new tests. The test powers were obtained using the Monte Carlo approach. Furthermore, the supremum of the calculation for \(J_{n, a}\) was acquired using a grid search on 1,000 equidistant points within the interval [0, 1].
Our findings revealed that the JEL and AJEL approaches proposed in [4] are less powerful than the classical approach when the testing is conducted using the original version of \(\vert I^{[1,1]}\vert\). In almost all cases, both \(R_{a}\) and \(J_{a}\) outperform the JEL and AJEL methods. We conclude that the novel tests demonstrate superior performance compared to the tests \(N_1^a\) and \(N_1^b\) proposed in [5]. When compared to EDF-based tests, the performance of the novel tests is better in some cases and comparable in others, both for median-based and maximum likelihood estimators.
In the case of large samples, the most natural way to compare tests is through the notion of asymptotic efficiency.
For a detailed review of the theory presented below, we refer the reader to the comprehensive work of Nikitin [6].
Let \(\mathcal{G}=\{g(x;\theta),\;\theta>0\}\) be a family of alternatives density functions, such that \(g(x;0)\) has the Lévy distribution with arbitrary scale parameter, and \(\int_{ \mathbb{R}^+ }\frac{1}{x^2}g(x;\theta)dx<\infty\) for \(\theta\) in the neighbourhood of 0, and some additional regularity conditions for U-statistics with non-degenerate kernels hold [7, 8]. Let also \(\{T_n\}\) and \(\{V_n\}\) be two sequences of test statistic that we want to compare.
Then for any alternative distribution from \(\mathcal{G}\) the relative Bahadur efficiency of the \(\{T_n\}\) with respect to \(\{V_n\}\) can be expressed as \[\begin{align*} e_{(T,V)}(\theta)=\frac{c_T(\theta)}{c_V(\theta)}, \end{align*}\] where \(c_{T}(\theta)\) and \(c_V(\theta)\) are the Bahadur exact slopes, functions proportional to the exponential rate of decrease of each test size when the sample size increases. It is usually assumed that \(\theta\) belongs to the neighborhood of 0, and in such cases, we refer to the local relative Bahadur efficiency of considered sequences of test statistics.
It is well known that for the Bahadur slope function Bahadur–Ragavacharri inequality holds [9], that is \[\begin{align*} c_T(\theta)\leq 2K(\theta), \end{align*}\] where \(K(\theta)\) is the minimal Kullback–Leibler distance from the alternative to the class of null hypotheses. This justifies the definition of the local absolute Bahadur efficiency by \[\begin{align}\label{effT} eff(T)=\lim_{\theta\to 0}\frac{c_T(\theta)}{2K(\theta)}. \end{align}\]
If the sequence \(\{T_{n}\}\) of test statistics under the alternative converges in probability to some finite function \(b(\theta)>0\) and the limit \[\label{ldf} \lim_{n\leftarrow\infty}n^{-1}\log P_{H_{0}}(T_{n}\geq t)=-f_{LD}(t) \] exists for any \(t\) in an open interval \(I\), on which \(f_{LD}\) is continuous and \(\{b(\theta),\theta>0\}\subset I\) then the Bahadur exact slope is equal to \[\begin{equation}\label{slope} c_{T}(\theta)=2f_{LD}(b(\theta)). \end{equation}\] However, in many instances, calculating the large deviation function, and consequently the Bahadur slope, proves to be an extremely challenging task.
In situations where the function \(c_T\) cannot be computed as \(\theta\) approaches zero, an alternative approach is to approximate the Bahadur slope as \(c_T^*(\theta)\). This approximate slope often closely coincides with the exact one. To calculate the approximate slope, we do not require the tail behavior of the distribution function of the statistics \(T_n\) but instead need the tail behavior of its limiting distribution, which is typically easier to determine.
Specifically, if the limiting distribution function of \(T_n\) under the null hypothesis \(H_0\) is denoted as \(F_T\), and its tail behavior is given by \(\log(1-F_T(t)) = -\frac{a_T^* t^2}{2}(1+o(1))\), where \(a_T^*\) is a positive real number, and the limit in probability of \(\frac{T_n}{\sqrt{n}}\) is denoted as \(b_T^*(\theta) > 0\), then the approximate Bahadur slope is equal to \(c_T^*(\theta) = a_T^*\cdot (b_T^*(\theta))^2\). For the calculation of the local approximate Bahadur slope, one can utilize Maclaurin expansion.
Our research findings, focusing solely on the case of the maximum likelihood estimator, revealed that the tuning parameter \(a\) significantly impacts the efficiency of \(R_a\) and \(J_a\). In all examined scenarios, the Bahadur efficiency of \(J_a\) decreases as \(a\) increases. However, this is not the case for the statistic \(R_a\). Based on our analysis, we concluded that the new statistics outperform the Bhati-Kattumanil one, with \(R_a\) exhibiting superior performance in terms of local approximate Bahadur efficiencies.
We applied the novel tests on two real datasets. The first one contained the weighted rainfall data for the month of January in India. The second dataset consisted of the well yields near Bel Air, Hartford county, Maryland.
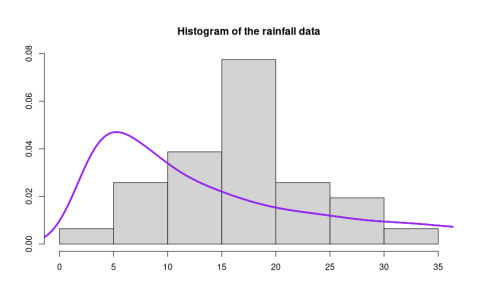
Figure: Histogram of rainfall application data and the appropriate Lévy density. The theoretical Lévy densities are drawn using the maximum likelihood estimate of the scale parameter \(\lambda\).
Based on
Žikica Lukić & Bojana Milošević (2023) Characterization-based approach for construction of goodness-of-fit test for Lévy distribution, Statistics, 57:5, 1087-1116, DOI: 10.1080/02331888.2023.2238236