Introduction
Abundant multivariate spatial data from the natural and environmental sciences demands research on the joint distribution of multiple spatially dependent variables (Wackernagel (2013), Cressie and Wikle (2011), Banerjee and Gelfand (2014)). Here, our goal is to estimate associations over spatial locations for each variable and those among the variables.
In this document, we will present an example of a simulated multivariate spatial data and how we can use Graphical Gaussian processes (GGP) (Dey and Banerjee (2021)) to model the data. First, we’ll introduce the general multivariate spatial model, and then we will introduce a variable graph and how to simulate a Graphical Gaussian process (Matérn) for that variable graph. Next, we will lay out the estimation steps of GGP parameters and how the estimated parameters compare against the truth.
Model
Let \(y(s)\) denote a \(q\times 1\) vector of spatially-indexed dependent outcomes for any location \(s \in \mathcal D \subset \mathbb{R}^d\) with typically \(d=2\) or \(3\). On our spatial domain \(\mathcal D\), a multivariate spatial regression model provides a marginal spatial regression model for each outcome as follows: \[\begin{equation} y_i(s) = x_i(s)^{T}\beta_i + w_i(s) + \epsilon_i(s)\;,\quad i=1,2,\ldots,q,\; s \in \mathcal D \tag{1} \end{equation}\] where \(y_i(s)\) is the \(i\)-th element of \(y(s)\), \(x_i(s)\) is a \(p_i\times 1\) vector of predictors, \(\beta_i\) is the \(p_i\times 1\) vector of slopes, \(w_i(s)\) is a spatially correlated process and \(\epsilon_i(s) \stackrel{ind}{\sim} N(0,\tau^2_i)\) is the random error in outcome \(i\). We usually assume that \(\epsilon_i(s)\) are independent across \(i\), whereas \(w(s)=(w_1(s), w_2(s),\ldots, w_q(s))^T\) is a zero-centred multivariate Gaussian process (GP) with a zero mean and a cross-covariance function that introduces dependency across space and among the \(q\) variables. Let \(\mathcal S_i\) represent the collection of places where the \(i-\)th variable was observed. The reference set of locations for our approach is \(\mathcal L = \cup_i\mathcal S_i\).
The definition of \(w(s)\) as the \(q \times 1\) multivariate graphical Matérn GP (Dey and Banerjee (2021)) with respect to a decomposable variable graph \({\mathcal G}_{\mathcal V}\) yields the distribution of each \(w_i\). The marginal parameters for each component Matérn process \(w_i(\cdot)\) are denoted by \(\{\phi_{ii}, \sigma_{ii} | i = 1.\ldots,q\}\).
It is sufficient to limit the intra-site covariance matrix \(\Sigma=(\sigma_{ij})\) to be of the following form to assure a valid multivariate Matérn cross-covariance function (Theorem 1 of Apanasovich and Sun (2012)):
\[\begin{equation} \begin{array}{cc} \nu_{ij} =& \frac 12 (\nu_{ii} + \nu_{jj}) + \Delta_A (1 - A_{ij}) \mbox{ where } \Delta_A \geq 0, A=(A_{ij}) \mbox{ for all } i \geq 0, A_{ii}=1 \\ \sum_{i,j} c_ic_j\phi_{ij} \leq 0 &\mbox{ is a conditionally non-negative definite matrix } \\ \sigma_{ij} =& b_{ij} \frac{\Gamma(\frac 12 (\nu_{ii}+\nu_{jj} + d))\Gamma(\nu_{ij})}{\phi_{ij}^{2\Delta_A+\nu_{ii}+\nu_{jj}}\Gamma(\nu_{ij} + \frac d2)} \mbox{ where } \Delta_A \geq 0, \mbox{ and } B=(b_{ij}) > 0, \mbox{ i.e., is p.d.} \end{array} \tag{2} \end{equation}\] This is equal to \(\Sigma = (B \odot (\gamma_{ij}))\), where \(\gamma_{ij}\)’s are constants collecting the components in (2) involving just \(\nu_{ij}\)’s and \(\phi_{ij}\)’s, and \(\odot\) indicates the Hadamard (element-wise) product.
In the following example, we’ll assume \(\Delta_A=0, \nu_{ij} = \frac{\nu_{ii}+\nu_{jj}}{2}\), \(\phi_{ij}^2 = \frac{\phi_{ii}^2 + \phi_{jj}^2}{2}\). The constraints in (2) simplifies to -
\[\begin{equation} \begin{array}{cc} \sigma_{ij} =& (\sigma_{ii} \sigma_{jj})^{\frac{1}{2}} * \frac{\phi_{ii}^{\nu_{ii}}\phi_{jj}^{\nu_{jj}}}{\phi_{ij}^{\nu_{ij}}} \frac{\Gamma(\nu_{ij})}{\Gamma(\nu_{ii})^{\frac 12} \Gamma(\nu_{ij})^{\frac 12}} r_{ij} \mbox{ where }, \mbox{ and } R=(r_{ij}) > 0, \mbox{ i.e., is p.d.} \end{array} \tag{3} \end{equation}\]
We also take \(\nu_{ii} = \nu_{jj} = 0.5\) in our case and hence, we only need to estimate the marginal scale (\(\phi_{ii}\)) and variance parameters (\(\sigma_{ii}\)) and cross-correlation parameters \(r_{ij}\). We also assume variable graph (\({\mathcal G}_{\mathcal V}\)) to be decomposable.
Simulation
As a first step of simulation, we need to fix a decomposable variable graph (\({\mathcal G}_{\mathcal V}\)). Depending on the perfect ordering of cliques in the graph, the density function of the full process can be factorized. Using this property, we can calculate the variance-covarinace matrix of the GGP and use it to simulate observation from a multivariate GGP.
Decomposable variable graph
If \(\mathcal G_\mathcal V\) is decomposable, it has a perfect clique sequence \(\{K_1,K_2,\cdots,K_p\}\) with separators \(\{S_2,\ldots,S_m\}\), and \(w(\mathcal L)\)’s joint density may be factorized as follows. \[\begin{equation} f_M(w(\mathcal L)) = \frac{\Pi_{m=1}^{p} f_C(w_{K_m}( \mathcal L))}{\Pi_{m=2}^{p} f_C(w_{S_m}( \mathcal L))}\;, \tag{4} \end{equation}\] where \(S_m=F_{m-1} \cap K_m\) and \(F_{m-1}= K_1 \cup \cdots \cup K_{m-1}\), and \(f_A\) denotes the the density of a GP over \(\mathcal L\) with covariance function \(A\) for \(A \in \{M,C\}\).
Here, we assume we have \(10\) variables with each being observed at \(250\) locations uniformly chosen from the \((0,1) \times (0,1)\) square. We assume the variable graph to be as follows.
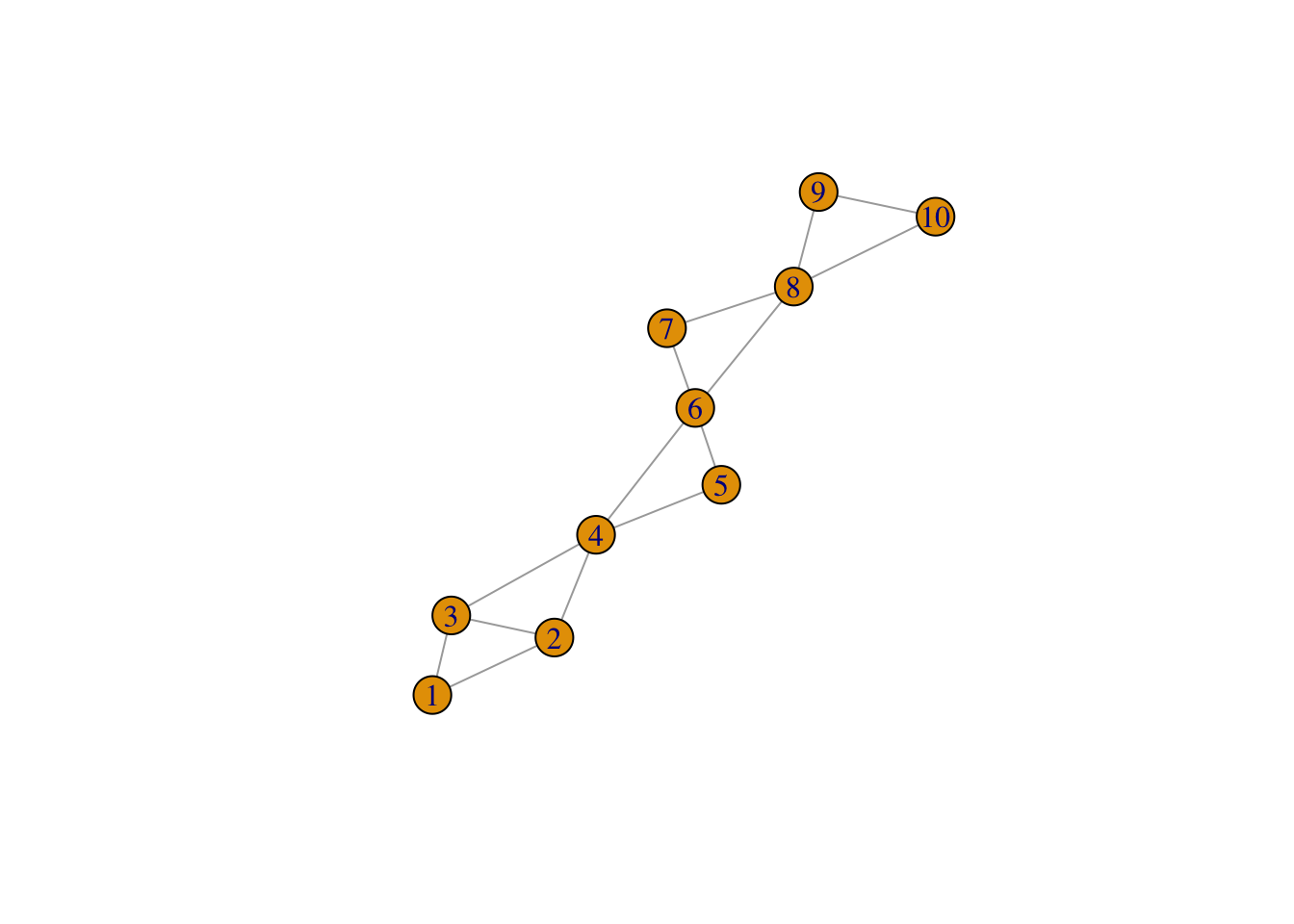
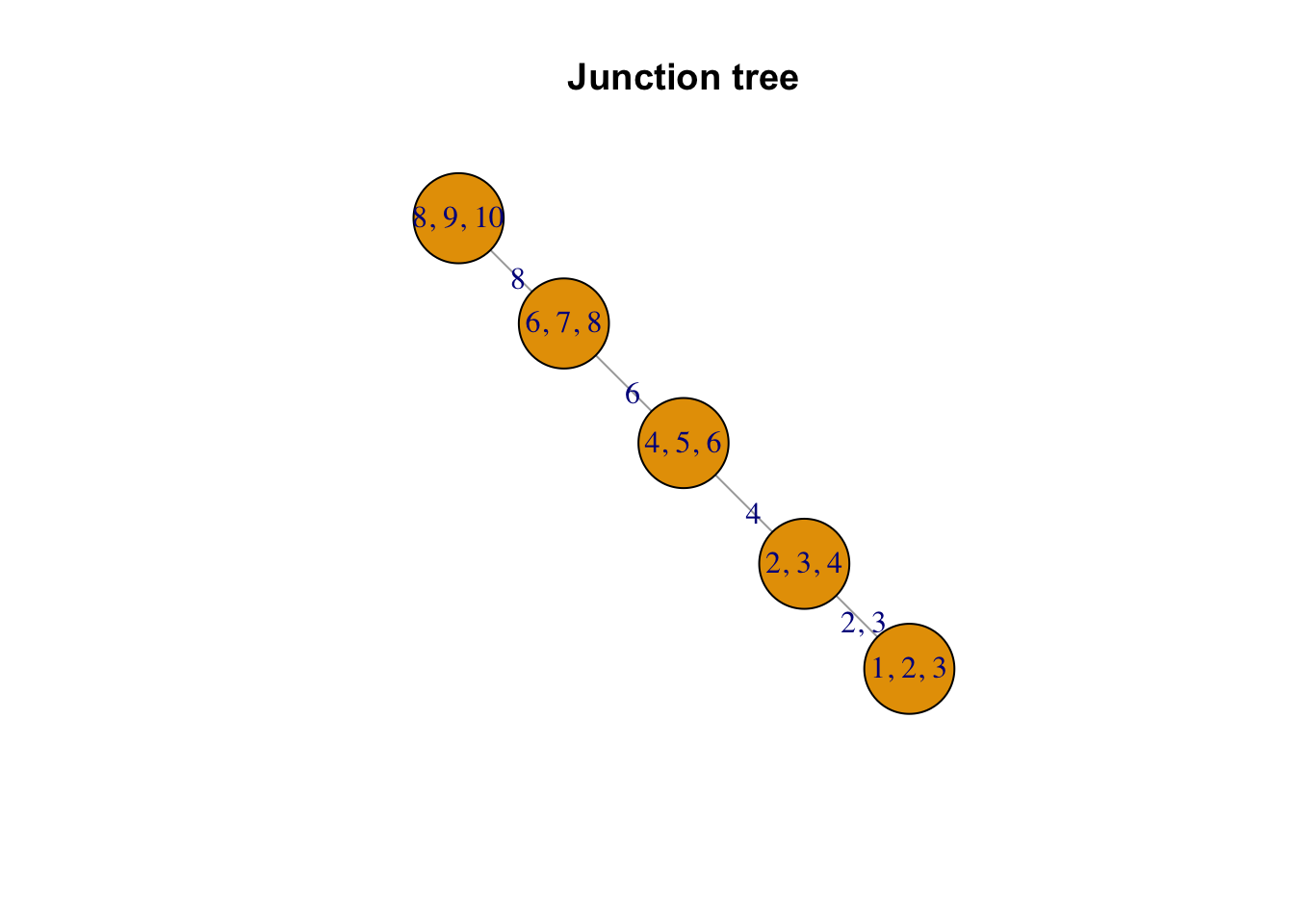
We calculate the perfect ordering of the cliques of the graph above and list the cliques and separators below. To visualize the decomposition, we also plot the junction tree (definition below) of the graph -
The junction graph \(G\) of a decomposable graph \(\mathcal G_\mathcal V\) is a complete graph with the cliques of \(\mathcal G_\mathcal V\) as its nodes. Every edge in the junction graph is denoted as a link, which is also the intersection of the two cliques, and can be empty. A spanning tree of a graph is defined as a subgraph comprising all the vertices of the original graph and is a tree (acyclic graph). If a spanning tree \(J\) of the junction graph of \(G\) satisfies the following property: for any two cliques \(C\) and \(D\) of the graph, every node in the unique path between \(C\) and \(D\) in the tree contains \(C \cap D\). Then \(J\) is called the junction tree for the graph \(\mathcal G_\mathcal V\). Here, the junction tree of the graph has the perfectly ordered cliques as its nodes and the separators denoted as edges.
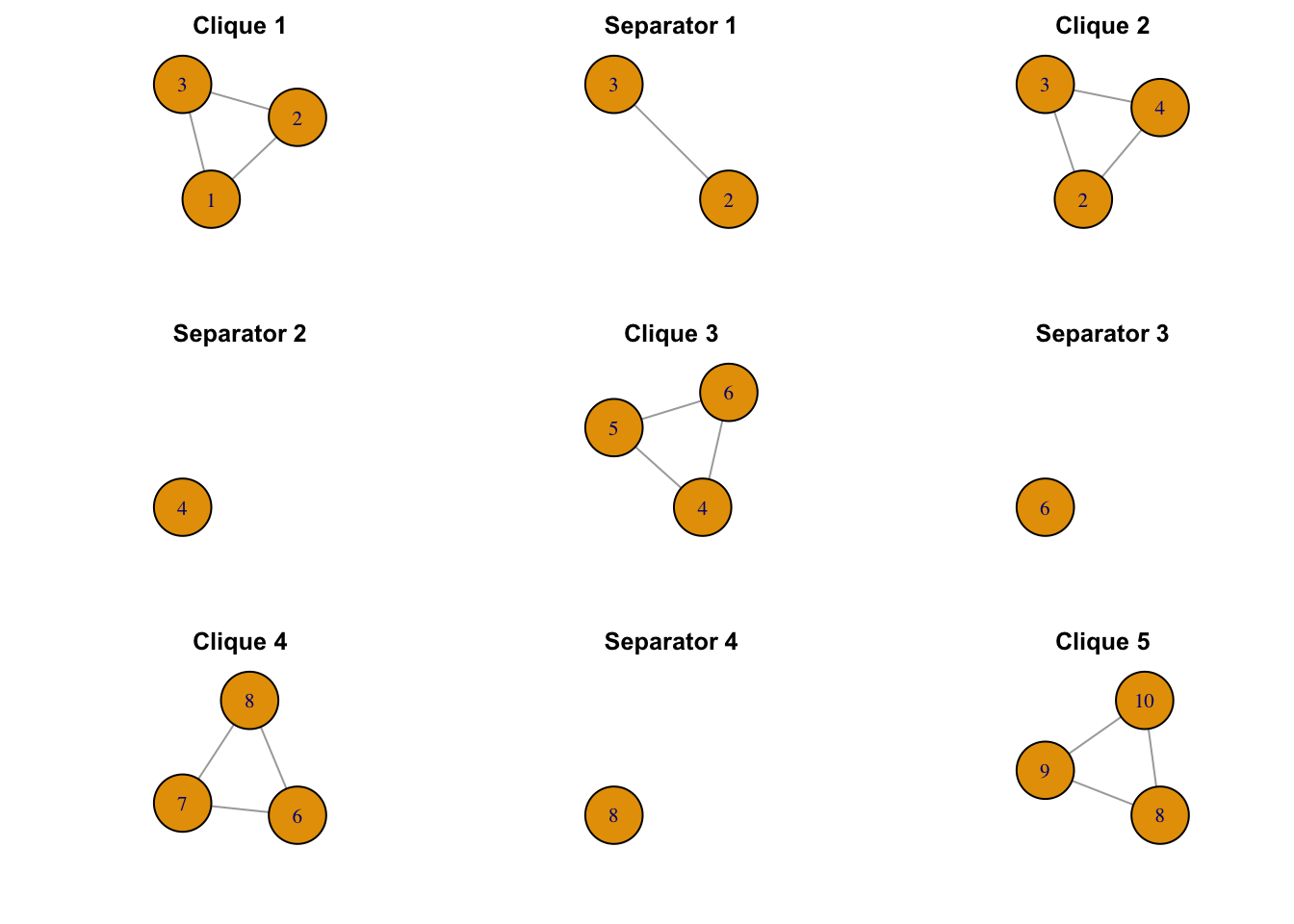
 Hence, in this case, the likelihood of the decomposable GGP would be as follows -
\[\begin{equation}
f_M(w(\mathcal L)) = \frac{f_C(w_{(1,2,3)}(\mathcal L)) f_C(w_{(2,3,4)}(\mathcal L)) f_C(w_{(4,5,6)}(\mathcal L)) f_C(w_{(6,7,8)}(\mathcal L)) f_C(w_{(8,9,10)}(\mathcal L))}{f_C(w_{(2,3)}(\mathcal L)) f_C(w_{(4)}(\mathcal L)) f_C(w_{(6)}(\mathcal L)) f_C(w_{(8)}(\mathcal L))}\;,
\tag{5}
\end{equation}\]
Hence, in this case, the likelihood of the decomposable GGP would be as follows -
\[\begin{equation}
f_M(w(\mathcal L)) = \frac{f_C(w_{(1,2,3)}(\mathcal L)) f_C(w_{(2,3,4)}(\mathcal L)) f_C(w_{(4,5,6)}(\mathcal L)) f_C(w_{(6,7,8)}(\mathcal L)) f_C(w_{(8,9,10)}(\mathcal L))}{f_C(w_{(2,3)}(\mathcal L)) f_C(w_{(4)}(\mathcal L)) f_C(w_{(6)}(\mathcal L)) f_C(w_{(8)}(\mathcal L))}\;,
\tag{5}
\end{equation}\]
Simulating latent GGP
First we fix the marginal and cross-covariance parameters of the process.
Now, the precision matrix of the GGP \(w(\mathcal L)\) satisfies (Lemma 5.5 of Lauritzen (1996)) \[\begin{equation} M(\mathcal L,\mathcal L)^{-1} = \sum_{m=1}^{p} [{C}_{[K_m \boxtimes \mathcal{G_L}]}^{-1}]^{\mathcal V \times \mathcal L} - \sum_{m=2}^{p} [{C}_{[S_m \boxtimes \mathcal{G_L}]}^{-1}] ^{\mathcal V \times \mathcal L}\;, %= \sum_{m=1}^{p} [{M}_{[K_m \boxtimes \mathcal{G_L}]}^{-1}] ^\mathcal V - \sum_{m=2}^{p} [{M}_{[S_m \boxtimes \mathcal{G_L}]}^{-1}] ^\mathcal V\; \tag{6} \end{equation}\]
The (6) and (4) shows that inverting the full cross-covariance matrix only requires inverting the clique and separator specific covariance matrices. Hence, the computational complexity for calculating likelihood of a multivariate GGP boils down to \(O(n^3 c^3)\) (here, \(O(250^3 * 27)\)) where \(c= 3\) is the maximum size of a clique in the perfect clique ordering of the graph. On the contrary, the likelihood of a full GGP would need \(O(n^3 q^3)\) complexity, i.e. \(O(250^3 * 1000)\) in our case.
We use the (6) to calculate the covariance of the latent GGP and we use it to simulate the latent process.
Simulating multivariate spatial outcome
Now we use (1) to simulate our multivariate outcome \(y_i(.), i= 1, \cdots, 10\). In order to do that, we fix some covariates \(x_i(\cdot)\) and simulate error process \(\epsilon_{i}(\cdot)\) independently from \(N(0,\tau^2_{ii})\). We take \(\tau_{ii}^2=\tau^2=0.25\) for all \(i\).
For analyzing the prediction accuracy of our method, we randomly pick \(20\%\) of the locations for each outcome variable and consider them missing. We will only be working with the training set to fit the model and judge our prediction accuracy on the test set.
Now we visualize the surface of the training data by variables below.
Data analysis
The analysis of our simulated data can be broken down in the following steps.
Marginal parameter estimation: We estimate the marginal scale (\(\phi_{ii}\)), variance (\(\sigma^2_{ii}\)) and smoothness parameters (\(\nu_{ii}\)) from the component Gaussian processes. We also estimate the error variance (\(\tau^2_{ii}\)) for each marginal processes.
Initialize Gibbs sampling: For this step, we need the following components:
- Processing the variable graph: We fix our variable graph for the estimation process. First we calculate cliques, separators of the graph. Then we color the nodes and edges of the graph for parallel computation purposes.
- Starting cross-correlation: We use the estimated marginal parameters and an initial correlation parameter to start off.
Gibbs sampling: We run our Gibbs sampler in two steps:
- Sampling latent spatial processes
- Sampling latent correlations
Marginal parameter estimation
- We first estimate the marginal process parameters using BRISC package in R. We estimate scale (\(\phi_{ii}\)) and variance (\(\sigma_{ii}\)) parameters. We fix the marginal smoothness (\(\nu_ii\)) and cross-smoothness (\(\nu_{ij}\)) parameters at \(0.5\).
- Same as the true cross-covariance, we calculate the cross-scale parameters as: \(\phi_{ij}= \sqrt{\frac{\phi_{ii}^2 + \phi_{jj}^2}{2}}\).
- We estimate the marginal regression coefficients (\(\beta_i\)).
- We estimate the marginal error variance (\(\tau_{ii}^2\)).
Initialize Gibbs sampling
- Process the variable graph:
First, we color the nodes of the variable graph. This will allow us to simulate the latent processes belonging to the same color in parallel.
We also construct a new graph \(\mathcal G_E(\mathcal G_V)=(E_\mathcal V,E^*)\) which denotes this graph on the set of edges \(E_\mathcal V\), i.e., there is an edge \(((i,j),(i',j'))\) in this new graph \(\mathcal G_E(\mathcal G_V)\) if \(\{i,i',j,j'\}\) are in some clique \(K\) of \(\mathcal G_V\). This allows us to facilitate parallel update of cross-correlation parameters corresponding to edges in the same color.
These two procedures are examples of chromatic Gibbs sampling.
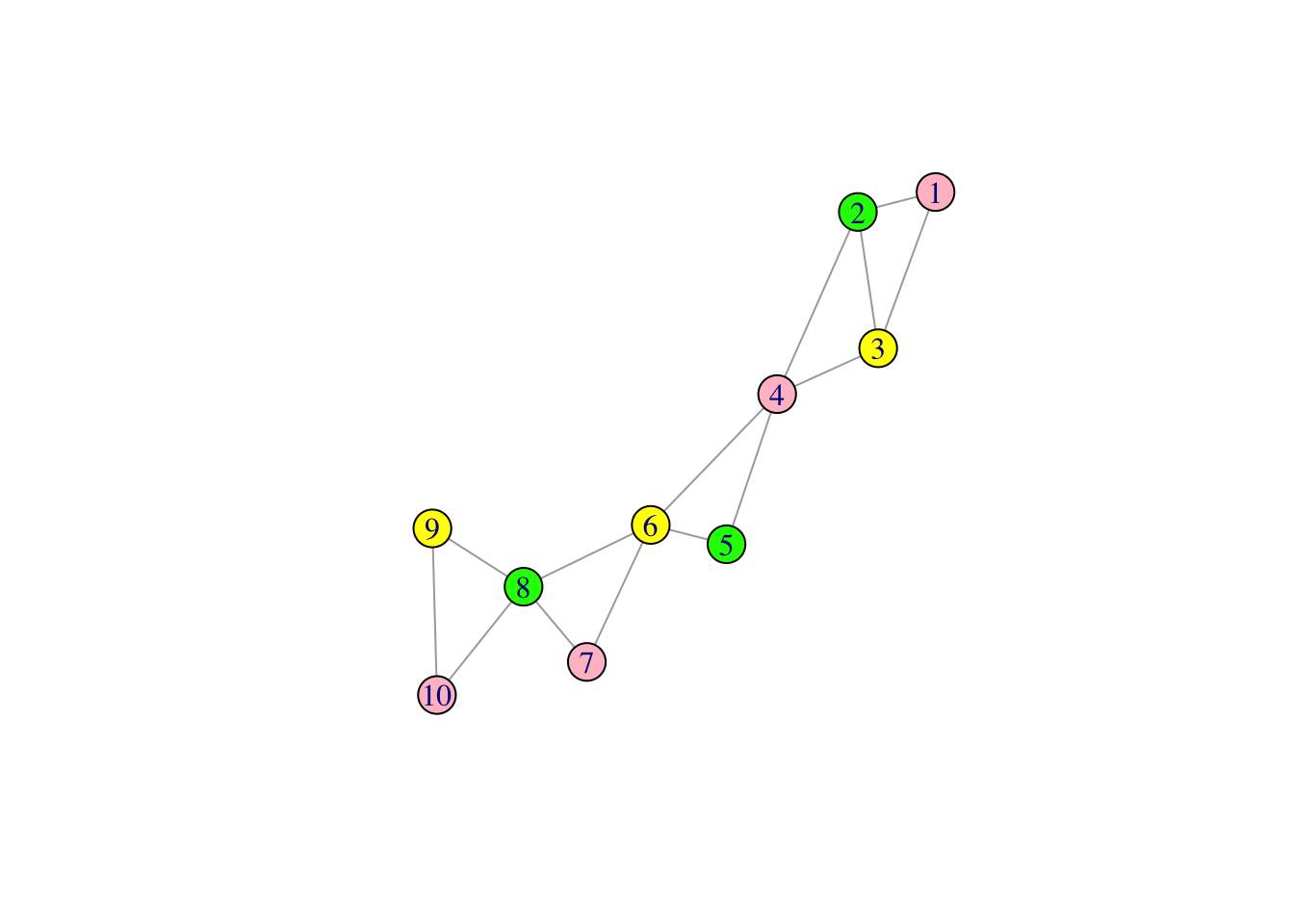
2.Calculate initial cross-covariance matrix: Start with an initial cross-correlation matrix. We Take a convex combination: \(0.5*diag(q) + 0.5*cor(Y.train)\). Then we use this initial cross-correlation parameters and estimated marginal parameters to store the cross covariance matrices for cliques and separators only.
The largest matrix we need to store is of size \(nq_c \times nq_c\) matrix where \(q_c\) is the size of maximum clique or separator).
Gibbs sampling
We iteratively perform the following steps until we reach a desired number of samples (\(N\)).
- Sampling latent processes : Using random draws from multivariate normal distribution
- Sampling correlations: Metropolis-hastings
- Jumping between graphs: Reversible jump MCMC.
Sampling latent processes
To update the latent random effects \(w\), let \(\mathcal L=\{s_1,\ldots,s_n\}\) and \(o_i=\mbox{diag}(I(s_1 \in \mathcal S_i), \ldots, I(s_n \in \mathcal S_i))\) denote the vector of missing observations for the \(i\)-th outcome. With \(X_{i}(\mathcal L) = (x_i(s_1),\ldots,x_i(s_n))^T\), \(y_i(\mathcal L)\) and \(w_i(\mathcal L)\) defined similarly, we obtain \[\begin{equation*} \begin{split} p(w_i(\mathcal L) | \cdot) & \sim N\left(\mathcal M_i^{-1}\mu_i, \mathcal M_i^{-1}\right)\;, \mbox{ where } \\ \mathcal M_i & =\frac{1}{\tau_i^2}\mbox{diag}(o_i) + \sum_{K \ni i}M_{\{i\} \times \mathcal L|(K\setminus \{i\}) \times \mathcal L}^{-1} - \sum_{S \ni i}M^{-1}_{\{i\} \times \mathcal L|(S\setminus \{i\}) \times \mathcal L}\;, \\ \mu_i &= \frac{(y_i(\mathcal L) - x_i(\mathcal L)^{T}\beta_i)\odot o_i}{\tau_i^2} + \\ & \qquad \sum_{K \ni i} T_{i}(K) w({(K\setminus \{i\}) \times \mathcal L}) - \sum_{S \ni i} T_i(S) w({(S\setminus \{i\}) \times \mathcal L})\;, \\ T_{i}(A) &= M_{\{i\} \times \mathcal L|(A\setminus \{i\}) \times \mathcal L}^{-1} M_{\{i\} \times \mathcal L,(A\setminus \{i\}) \times \mathcal L}M_{(A\setminus \{i\}) \times \mathcal L}^{-1}, \mbox{ for } A \in \{K,S\}.\\ % U_i(S) &= M_{\{i\} \times \mathcal L|(S\setminus \{i\}) \times \mathcal L}^{-1} M_{(S\setminus \{i\}) \times \mathcal L,\{i\} \times \mathcal L}M_{(S\setminus \{i\}) \times \mathcal L}^{-1}. \end{split}\label{eqn: gibbs-sam-latent} \end{equation*}\]
%We denote \(\mathscr T_i= \mathcal L \setminus \mathscr S_i\). % for a clique \(K\) in variable graph \(\mathcal{G_V}\), the set - \(K \times \mathcal L = K \times \mathscr S\), \(S \times \mathcal L= S \times \mathscr S\), %\(i_{K}=\{K \setminus i\} \times \mathscr S\), \(i \times \mathscr S_i = i_{\mathscr S}\) and \(i \times \mathscr T_i= i_{\mathscr T}\), \(i_{K} \cup i_{\mathscr T}= i_{K\mathscr T}\) and \(i_{K} \cup i_{\mathscr S}= i_{K \times \mathcal L}\) . Also, for a clique \(K\) in containing a variable \(i\), let’s denote \(M_{i_{{\mathscr S}.K}} = M_{i_{\mathscr S}} - M_{i_{\mathscr S}, i_{K\mathscr T}}M_{i_{K\mathscr T}}^{-1}M_{i_{K\mathscr T},i_{\mathscr S}}\) and \(M_{i_{{\mathscr T}.K}} = M_{i_{\mathscr T}} - M_{i_{\mathscr T}, i_{K \times \mathcal L}}M_{i_{K \times \mathcal L}}^{-1}M_{i_{K \times \mathcal L},i_{\mathscr T}}\).
Sampling cross-correlation parameters
Requires only checking positive-definiteness of the clique-specific cross-covariance matrix and inverting it. The largest matrix inversion across all these updates is of the order \(nc \times nc\), corresponding to the largest clique. The largest matrix that needs storing is also of dimension \(nc \times nc\). These result in appreciable reduction of computations from any multivariate Matérn model that involves \(nq \times nq\) matrices and positive-definiteness checks for \(q \times q\) matrices at every iteration.
For every correlation parameter corresponding to edges in the current graph, we draw a new correlation value from the proposal distribution.
We accept or reject the proposal based on the Metropolis-Hastings acceptance probability.
Results
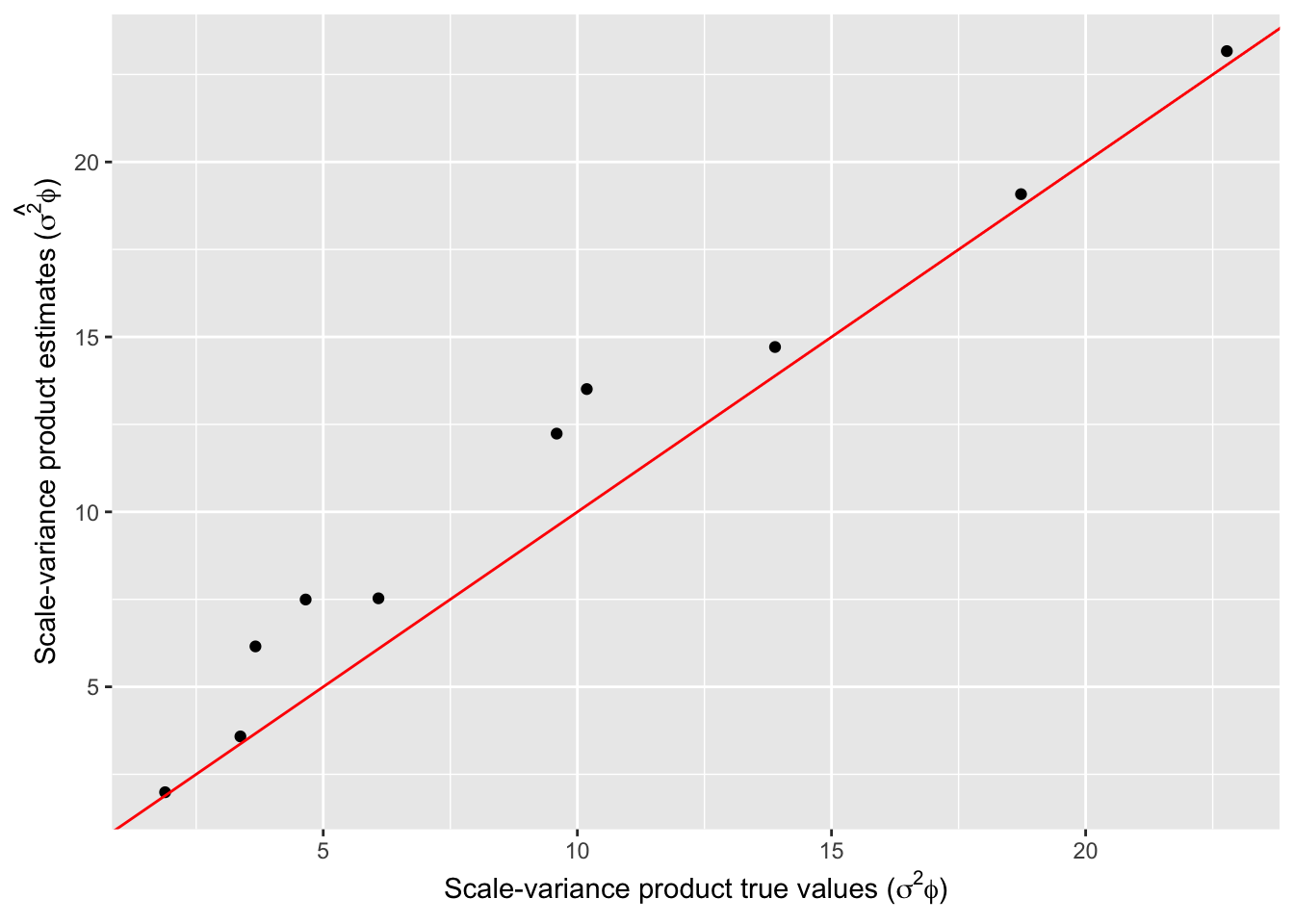
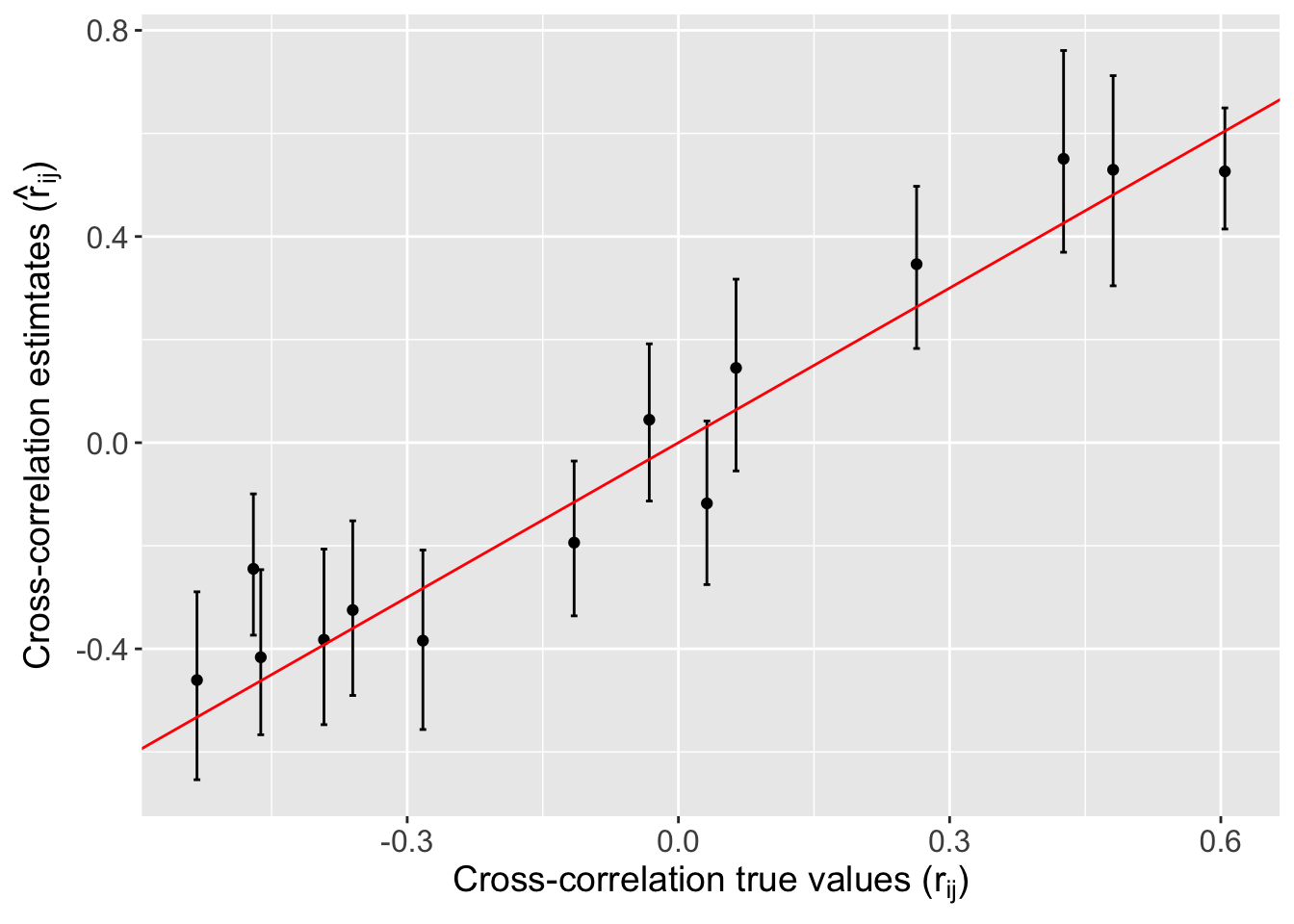
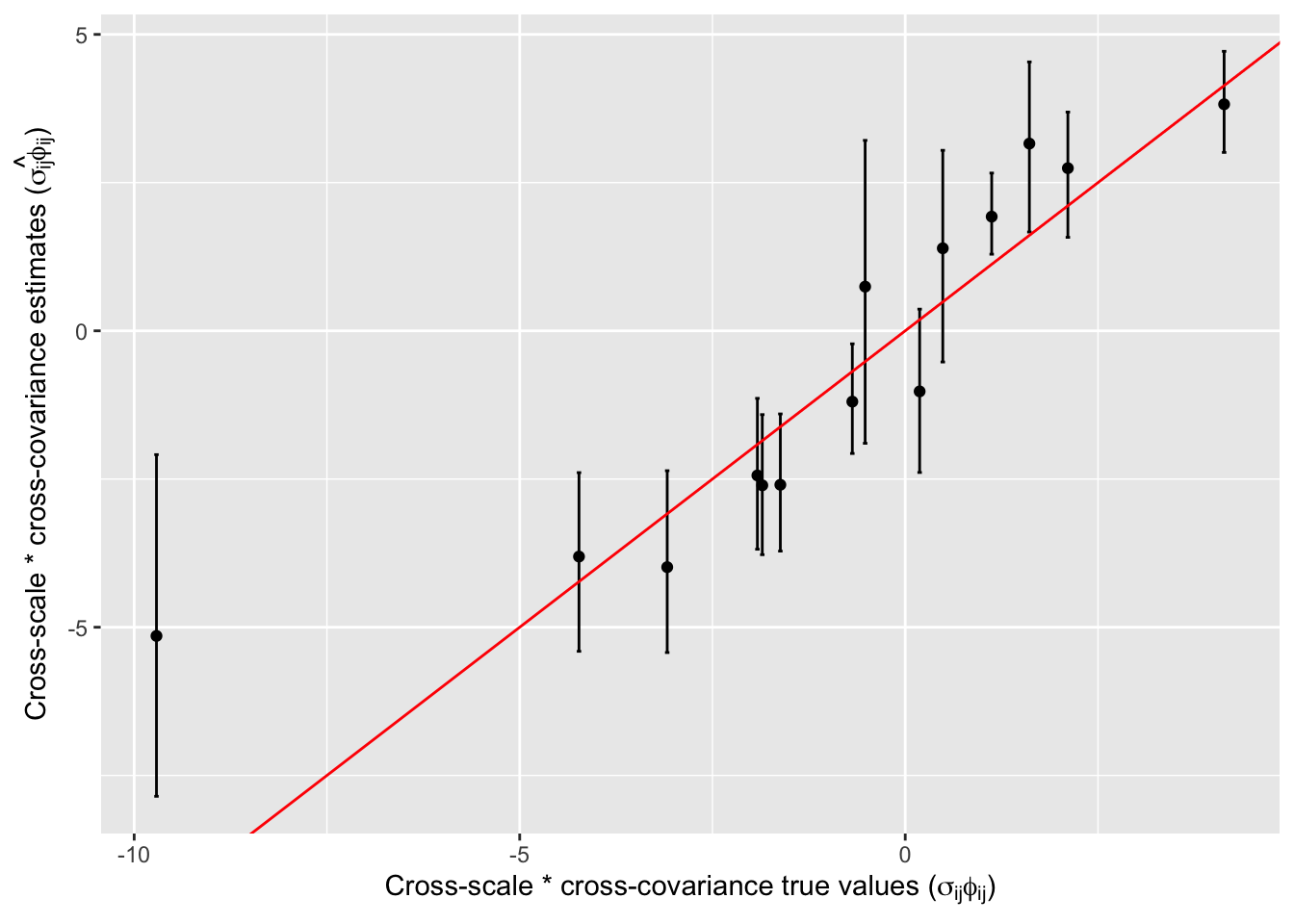
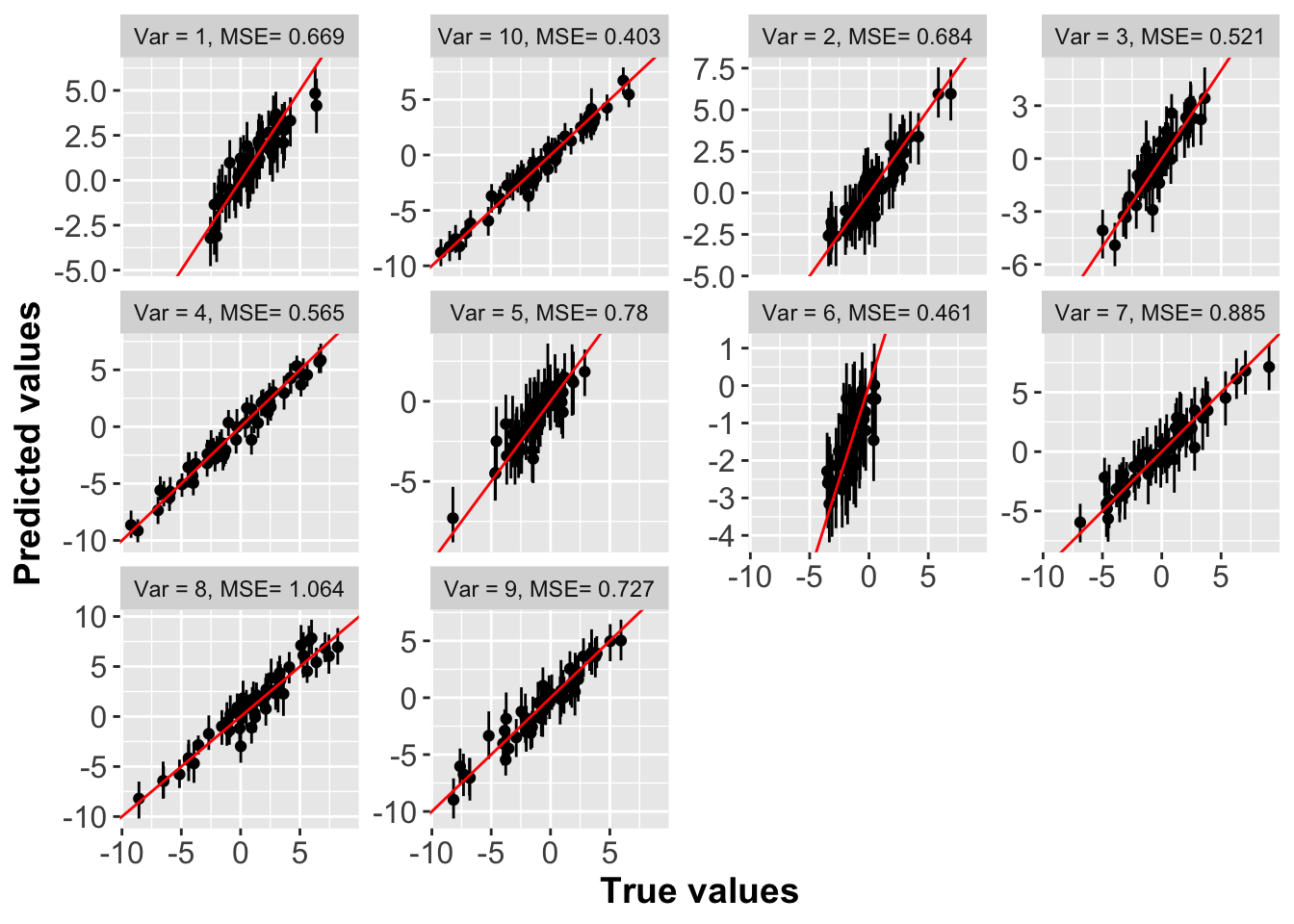
We create three plots below among true and estimated parameters for - (1) product of marginal scale and variance parameter (\(\sigma_{ii}\)), (2) cross-correlation parameter (\(r_{ij}\)) and (3) product of cross-covariance and cross-scale parameter (\(\sigma_{ij}*\phi_{ij}\)). The points on all the plots align on the \(y=x\) line thus showing the accuracy of our estimation. We also create a plot across \(10\) variables showing true test data values and predicted values from our model. The points align on \(y=x\) line and mean-square error varied from \(0.403\) to \(1.064\).