Meanders, monotone meanders, and Baxter permutations
Versions of the following question can be traced back at least to the work of Henri Poincaré (Poincaré (1912)):
In how many ways a simple loop in the plane can cross a line a specified number of times?
Despite many efforts, this question remains open after more than a century. Let us start by mathematically formalizing the latter question.
Definition 1.1. A meander of size \(n\in\mathbb{N}\) is a simple loop \(\ell\) (i.e., a homeomorphic image of the circle) in \(\mathbb{R^2}\) which crosses the real line \(\mathbb{R}\) exactly \(2n\) times and does not touch the line without crossing it, viewed modulo orientation-preserving homeomorphisms from \(\mathbb{R^2}\) to \(\mathbb{R^2}\) which take \(\mathbb{R}\) to \(\mathbb{R}\).
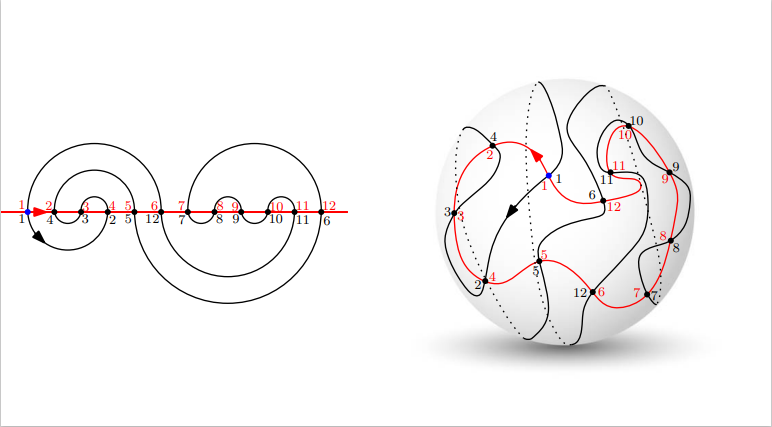
Figure 1: Left: A meander of size \(6\), with the intersection points of the loop and the line labeled by the order in which they are hit by the loop (in black) and the line (in red) starting at the blue vertex. The associated meandric permutation is \(\sigma_{\ell}=1,4,3,2,5,12,7,8,9,10,11,6\) (in one-line notation); see Definition 1.1. Right: The same meander of size \(6\) seen as a pair of Jordan curves in the sphere.
See the left-hand sides of Figures 1 and 2 for some illustrations of meanders. A meander of size \(n\) can equivalently be thought of as a pair of Jordan curves in the sphere which intersect exactly \(2n\) times and which do not intersect without crossing, viewed modulo orientation-preserving homeomorphisms from the sphere to itself. The correspondence with Definition 1.1 is obtained by viewing \(\mathbb{R}\) as a curve in the Riemann sphere. See the right-hand side of Figure 1.
Each meander can be bijectively encoded with the corresponding meandric permutation.
Definition 1.2. For a meander \(\ell\) of size \(n\), the corresponding meandric permutation \(\sigma_{\ell}\) is the permutation of \([1,2n]\cap\mathbb{Z}\) obtained as follows. Order the \(2n\) intersection points of \(\ell\) with \(\mathbb{R}\) from left to right. Then, consider the second order in which these intersection points are hit by \(\ell\) when we start \(\ell\) from the leftmost intersection point and traverse it counterclockwise. Then \(\sigma_\ell (i)=j\) if some intersection point is the \(i\)-th visited point by the first order and the \(j\)-th visited point by the second one.
See Figure 1 for an example and the right-hand side of Figure 2 for the plots of two large uniform meandric permutations. Note that any meandric permutation fixes 1. It is easily verified that the mapping \(\ell\mapsto\sigma_{\ell}\) is a bijection from the set of meanders of size \(n\) to the set of meandric permutations of size \(2n\). The study of meandric permutations dates back to at least the paper Rosenstiehl (1984), where they are called “planar permutations”.
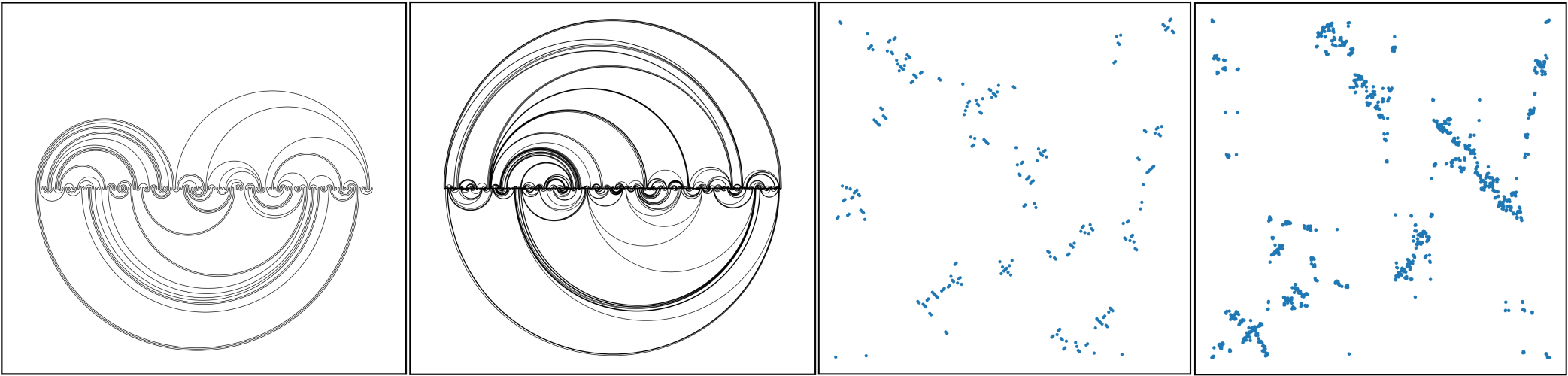
Figure 2: Left: Two large uniform meanders \(\ell\) of size 256 and 2048. Right: The plots of the two corresponding meandric permutations \(\sigma_{\ell}\); the blue dots correspond to the values \((i,\sigma_\ell(i))_{i = 1,\dots,|\sigma_\ell|}\). These simulations are obtained using the Markov chain Monte Carlo algorithm from Heitsch and Tetali (2011).
The term “meander” was first coined by Arnold (1988). Meanders are of interest in physics and computational biology as models of polymer folding Di Francesco, Golinelli, and Guitter (1997). There is a vast mathematical literature devoted to the enumeration of various types of meanders, which has connections to many different subjects, from combinatorics to theoretical physics and more recently to the geometry of moduli spaces (Delecroix et al. (2020)). See Zvonkin (2021) for a brief recent survey of this literature and La Croix (2003) for a more detailed account. Additionally, meanders are the connected components of meandric systems, recently studied in Curien et al. (2019), Kargin (2020), Goulden, Nica, and Puder (2020), Féray and Thévenin (2022), Fukuda and Nechita (2019), Borga, Gwynne, and Park (2022).
The problem of enumerating all meanders of size \(n\) – this is the Question (1.1) – is open and seemingly quite difficult. But, it was conjectured by Di Francesco, Golinelli, and Guitter (Di Francesco, Golinelli, and Guitter (2000)) that the number of meanders of size \(n\) behaves asymptotically like \(C \cdot A^n n^{-\alpha}\), where \(\alpha = (29 + \sqrt{145})/12\). This conjecture was later numerically tested by Jensen and Gutmann (Jensen and Guttmann (2000)), where they also proposed the numerical estimate of \(A \approx 12.26\). The best known rigorous bounds for the constant \(A\) are \(11.380\leq A \leq 12.901\), as proved in Albert and Paterson (2005).
A candidate scaling limit for meanders and meandric permutations was recently proposed and studied in Borga, Gwynne, and Sun (2022).
In this paper, we will address a simpler but very related model, i.e.monotone meanders.
Definition 1.3. A monotone meander of size \(n\in\mathbb{N}\) is a pair of simple curves \(\ell_1\) and \(\ell_2\) in \([0,1]^2\) which cross each other exactly \(2n-1\) times and such that:
\(\ell_1\) starts on the left-hand side of \([0,1]^2\), ends on the right-hand side of \([0,1]^2\) and never moves in the left direction. (Equivalently, it is the graph of a continuous function from \([0,1]\) to \([0,1]\).)
\(\ell_2\) starts on the bottom side of \([0,1]^2\), ends on the top side of \([0,1]^2\) and never moves in the bottom direction. (Equivalently, it is the graph of a continuous function from \([0,1]\) to \([0,1]\) rotated by 90 degrees.)
As in the case of meanders, to each monotone meander we can associate the corresponding monotone meandric permutation. Two monotone meanders are equivalent if they induce the same monotone meandric permutation.
See Figure 3 for an example. Note that a monotone meandric permutation maps even numbers to even numbers, and odd numbers to odd numbers. The permutation mapping odd numbers is called a Baxter permutation, while the permutation mapping even numbers is called a reduced Baxter permutation. It can be shown Baxter (1964), William M. Boyce (1967), William Martin Boyce (1981) that the Baxter permutation corresponding to a monotone meandric permutation uniquely determine the monotone meandric permutation itself. Hence there is a natural bijection between monotone meandric permutations and Baxter permutations.
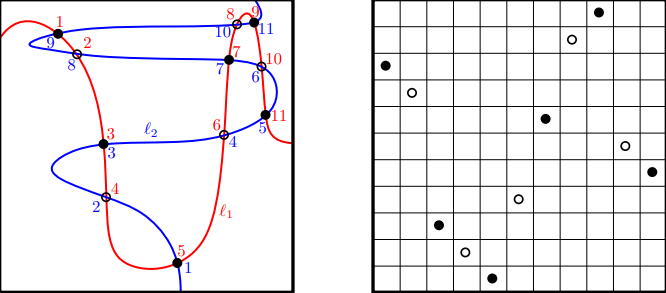
Figure 3: Left: A monotone meander of size \(6\), with the intersection points labeled by the order in which they are hit by the curve \(\ell_1\) (in red) and the curve \(\ell_2\) (in blue). Right: The associated monotone meandric permutation: the Baxter permutation corresponds to the black dots, while the reduced Baxter permutation corresponds to the white dots.
Baxter permutations were introduced by Glen Baxter in 1964 Baxter (1964) while studying fixed points of commuting functions. They are classical examples of pattern-avoiding permutations, which have been intensively studied both in the probabilistic and combinatorial literature (see e.g. William M. Boyce (1967), Chung et al. (1978), Mallows (1979), Bousquet-Mélou (2002/03), Canary (2010), Felsner et al. (2011), Bouvel et al. (2018)). They are known to be connected with various other interesting combinatorial structures, such as bipolar orientations Bonichon, Bousquet-Mélou, and Fusy (2010), walks in cones Kenyon et al. (2019), certain pairs of binary trees and a family of triples of non-intersecting lattice paths Felsner et al. (2011), and domino tilings of Aztec diamonds Canary (2010).
The diagrams of two large uniform Baxter permutations is plotted in Figure 4.

Figure 4: The diagrams of two uniform Baxter permutations of size 3253 and 4520.
Main results: the permuton limit of Baxter permutations and its intensity measure
In recent years there has been an increasing interest in studying limits of random non-uniform permutations. One approach is to look at the convergence of relevant statistics, such as the number of cycles, the number of inversions, or the length of the longest increasing subsequence. For a brief overview of this approach see e.g. Borga (2021a).
The more recent approach is to directly determine the scaling limits of permutation diagrams. Here given a permutation \(\sigma\) of size \(n\), its diagram is a \(n \times n\) table with \(n\) points at position \((i,\sigma(i))\) for all \(i\in[n]:=\{1,2,\dots,n\}\). (See the right-hand side of Figure 3 for an example.) Their scaling limits are called permutons. See e.g. Borga (2021a) for an overview of this approach.
Definition 2.1. A Borel probability measure \(\mu\) on the unit square \([0,1]^2\) is a permuton if both of its marginals are uniform, i.e., \(\mu([a,b]\times[0,1]) = \mu([0,1]\times[a,b])=b-a\) for any \(0\le a<b\le 1\). A permutation \(\sigma\) can be viewed as a permuton \(\mu_{\sigma}\) by uniformly distributing mass to the squares \(\{[\frac{i-1}{n}, \frac{i}{n}]\times [\frac{\sigma(i)-1}{n}, \frac{\sigma(i)}{n}]: i \in [n]\}.\) More precisely, \[\begin{equation*} \mu_\sigma(A) = n \sum_{i=1}^n Leb \big([(i-1)/n, i/n] \times [(\sigma(i)-1)/n,\sigma(i)/n] \cap A\big), \end{equation*}\] where \(A\) is a Borel measurable set of \([0,1]^2\).
For a deterministic sequence of permutations \(\sigma_n\), we say that \(\sigma_n\) converge in the permuton sense to a limiting permuton \(\mu\), if the permutons \(\mu_{\sigma_n}\) induced by \(\sigma_n\) converge weakly to \(\mu\). The set of permutons equipped with the topology of weak convergence of measures can be viewed as a compact metric space.
Dokos and Pak (2014) studied the expected limiting permuton of the so-called doubly alternating Baxter permutations. The authors raised the question of proving the existence of the Baxter permuton as the scaling limit of uniform Baxter permutations, and determine its expected density. The existence of the Baxter permuton was established in Borga and Maazoun (2022a).
Theorem 2.2 (Borga and Maazoun (2022b), Theorem 1.9) Let \(\sigma_n\) be a uniform Baxter permutation of size \(n\). The following convergence w.r.t. the permuton topology holds: \(\mu_{\sigma_n}\) \(\xrightarrow{d}\) \(\mu_B\) where \(\mu_B\) is a random permuton called the Baxter permuton.
Remark 2.3. In Borga (2021b), a two-parameter family of permutons called the skew Brownian permuton was introduced. This family includes the Baxter permuton and a well-studied one-parameter family of permutons, called the biased Brownian separable permuton (Bassino et al. (2018), Bassino et al. (2020)), as special cases.
The Baxter permuton \(\mu_B\) is a random probability measure on the unit square (with uniform marginals); recall Figure 4. The next result is an explicit expression of its intensity measure, defined by \(\mathbb E [\mu_{B}](\cdot):=\mathbb E [\mu_{B}(\cdot)]\), which answers Dokos and Pak (2014).
Theorem 2.4. (Borga et al. (2023), Theorem 1.3) Consider the Baxter permuton \(\mu_B\). Define the function \[\begin{equation}\label{eqn-rho} \rho(t, x, r):= \frac{1}{t^2} \left(\left(\frac{3rx}{2t}-1\right)e^{-\frac{r^2+x^2-rx}{2t}}+e^{-\frac{(x+r)^2}{2t}}\right). \end{equation}\] Then the intensity measure \(\mathbb E [\mu_B]\) is absolutely continuous with respect to the Lebesgue measure on \([0,1]^2\). {Moreover}, it has the following density function \[\begin{equation}\label{eqn-baxter-density} p_B(x, y) = c\int_{\max\{0, x+y-1\}}^{\min\{x, y\}}\int_{\mathbb R_{+}^4}\rho(y-z, \ell_1, \ell_2)\rho(z, \ell_2, \ell_3)\rho(x-z, \ell_3, \ell_4)\rho(1+z-x-y, \ell_4, \ell_1)\,\ d\ell_1 d\ell_2 d\ell_3 d\ell_4\, dz, \end{equation}\] where \(c\) is a normalizing constant.
We remark that, further computation of the integral (2.2) is tricky, as it involves integrating a four-dimensional Gaussian in the first quadrant. We also recall that the intensity measure of other universal random limiting permutons has been investigated in the literature. For instance, the intensity measure of the biased Brownian separable permuton, was determined by Maazoun in Maazoun (2020). We recall that the biased Brownian separable permuton \(\mu^q_S\), defined for all \(q\in[0,1]\), is a one-parameter universal family of limiting permutons arising form pattern-avoiding permutations. In Maazoun (2020), it was proved that for all \(q\in(0,1)\), the intensity measure \(\mathbb E[\mu^q_S]\) of the biased Brownian separable permuton is absolutely continuous with respect to the Lebesgue measure on \([0,1]^2\). Furthermore, \(\mathbb E[\mu^q_S]\) has the following density function
\[\begin{equation*} p^q_S(x, y) =\int_{\max\{0,x+y -1\}}^{\min\{x,y\}} \frac{3q^2(1-q)^2 \,da } {2\pi(a(x-a)(1-x-y+a)(y-a))^{3/2}{\left(\frac{q^2}{a}+\frac{(1-q)^2}{(x-a)}+\frac{q^2}{(1-x-y+a)}+\frac{(1-q)^2}{(y-a)}\right)^{5/2}}}. \end{equation*}\] The proof of Maazoun (2020) relies on an explicit construction of the biased Brownian separable permuton \(\mu^q_S\) from a one-dimensional Brownian excursion decorated with i.i.d. plus and minus signs. To the best of our knowledge this proof cannot be easily extended to the Baxter permuton case. Our proof of Theorem 2.4 uses the combination of two main achievements:
A connection (Borga (2021b)) between the Baxter permuton (and more generally the skew Brownian permuton of Remark 2.3) and some well-known families of random curves and random surfaces: the Schramm-Loewner evolution (SLE) curves and the Liouville quantum gravity (LQG) spheres.
Some integrability results (Ang, Holden, and Sun (2020)) for SLE curves and LQG spheres which go under the name of conformal welding of quantum surfaces.
Explaining the results above would require a long digression; hence we just conclude this article with some plots of \(p_B(x, y)\) and \(p^q_S(x, y)\) using numerical approximations of the integrals.

Figure 5: From left to right: The diagrams of the densities \(p_S^{0.1}(x,y)\), \(p_S^{0.4}(x,y)\), \(p_S^{0.5}(x,y)\), and \(p_B(x,y)\).
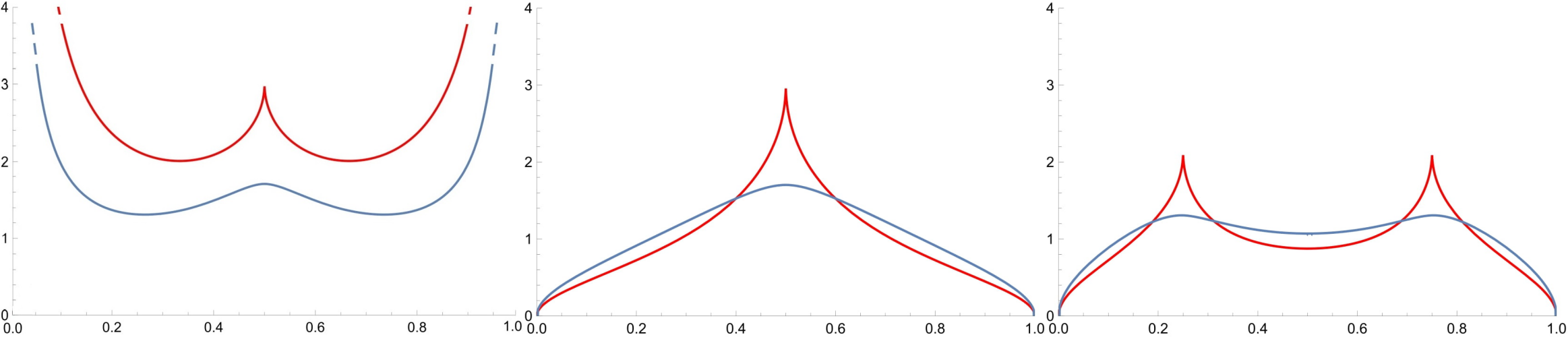
Figure 6: Some sections of the densities \(p_S^{0.5}(x,y)\) and \(p_B(x,y)\). From left to right: In red (resp. in blue) we plot the diagrams of \(p_S^{0.5}(x,x)\) (resp. \(p_B(x,x)\)), \(p_S^{0.5}(x,1/2)\) (resp. \(p_B(x,1/2)\)), and \(p_S^{0.5}(x,1/4)\) (resp. \(p_B(x,1/4)\)).