Passive scalar turbulence is the study of how a scalar quantity, such as temperature or salinity, is transported by an incompressible fluid. This process is modeled by the advection diffusion equation \[\begin{equation} \partial_tg_t + u_t\cdot\nabla g_t - \kappa \Delta g_t = s_t,\label{eqAD}\tag{AD} \end{equation}\] where \(g_t\) is the scalar quantity, \(u_t\) is an incompressible velocity field, \(\kappa>0\) is the diffusivity parameter and \(s_t\) is a replenishing source. As \(g_t\) evolves, it often settles into a statistical steady state and complex self-similar structures arise due to repeated stretching and folding by the velocity field.
Figure 1: A numerical simulation of scalar turbulence on \(\mathbb{T}^2\) advected by the stochastic Navier-Stokes equations (all rights to the video content belong to Sam Punshon-Smith).
In his 1959 work (Batchelor (1959)) Batchelor made a significant step toward understanding these structures. He predicted that, on average, the \(L^2\) power spectral density of \(g_t\) displays a \(|k|^{-1}\) power law (Batchelor’s law) for the \(L^2\) power spectral density of \(g_t\) along frequencies \(k\) in the so-called viscous convective range, i.e., length-scales sufficiently small such that the fluid motion is viscosity-dominated but large enough so as not to be dissipated by molecular diffusion. This law has since been verified in physical, numerical, and experimental settings (e.g. Grant et al. (1968), Antonia and Orlandi (2003), Gibson and Schwarz (1963)) and is frequently used by scientists to predict the distribution of pollutants and biological matter in the ocean and atmosphere. Despite this success, Batchelor’s law has evaded rigorous mathematical proof.
The purpose of this post is to report progress with Jacob Bedrossian and Alex Blumenthal on the development of rigorous mathematical tools for studying Batchelor’s law when \(u_t\) evolves according to a randomly forced fluid model. The primary example is the incompressible stochastic Navier-Stokes equations on \(\mathbb{T}^2\),
\[\begin{equation} \partial_t u_t + u_t\cdot\nabla u_t + \nabla p_t - \nu \Delta u_t = \xi_t, \\ \mathbf{div} u_t=0,\label{eqSNS}\tag{SNS} \end{equation}\]though other well-posed models (not restricted two dimensions) can be considered. Here the stochastic forcing \(\xi_t\) is assumed to be a non-degenerate, white-in-time, spatially Sobolev regular Gaussian forcing. The viscosity parameter \(\nu > 0\) can be considered the inverse Reynolds number.
For this model and a host of other fluid models, in Bedrossian, Blumenthal, and Punshon-Smith (2019a) we prove a version Batchelor’s prediction on the cumulative power spectrum, when the viscosity parameter \(\nu>0\) is fixed.
Theorem 1 (Bedrossian, Blumenthal, and Punshon-Smith 2019a):
Let \(\Pi_{\leq N}\) denote the projection onto Fourier modes with \(|k|\leq N\). Let the source \(s_t\) in \(\eqref{eqAD}\) be a white-in-time Gaussian process and \(u_t\) be given by \(\eqref{eqSNS}\) as described above. Then there exists a unique stationary probability measure \(\mu^\kappa\) for the Markov process \((u_t,g_t)\) and \(\kappa\)-independent constants \(C \geq 1\) and \(\ell_0\leq 1\) such that
\[\begin{equation} \frac{1}{C_0}\log N \leq \mathbb{E}_{\mu^\kappa} \|\Pi_{\leq N}g\|^{2}_{L^2} \leq C_0\log N \quad \text{for}\quad \ell_{0}^{-1} \leq |k|\leq \kappa^{-1/2}.\label{eqBL}\tag{BL} \end{equation}\]Uniform-in-\(\kappa\) exponential mixing and Batchelor’s law
The key ingredient in obtaining Batchelor’s law is the mixing properties of the velocity field \(u_t\), and a quantitative understanding of how that mixing interacts with the diffusion. In the absence of a scalar source (\(s_t =0\)) and molecular diffusivity (\(\kappa = 0\)), the velocity field \(u_t\) filaments \(g_t\) and forms small scales as it homogenizes, a process known as mixing (see Figure 2).
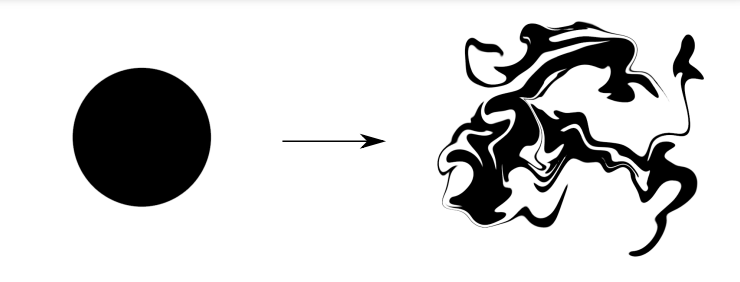
Figure 2: Mixing of a circular blob, showing filamentation and formation of small scales.
Mixing of the scalar \(g_t\) (assuming it is mean zero) can be quantified using a negative Sobolev norm. Commonly chosen is the \(H^{-1}\) norm \(\|g_t\|_{H^{-1}} := \|(-\Delta)^{-1/2}g_t\|_{L^2}\), which essentially measures the average filamentation width, though there are many other expedient choices Thiffeault (2012).
In Bedrossian, Blumenthal, and Punshon-Smith (2021) we show that solutions to \(\eqref{eqSNS}\) cause the advection diffusion equation (without source but with diffusion) to mix exponentially fast with a rate that is uniform in the diffusivity parameter \(\kappa\).
Theorem 2 (Uniform-in-diffusivity mixing, Bedrossian, Blumenthal, and Punshon-Smith 2021):
Let \(u_t\) solve \(\eqref{eqSNS}\) with non-degenerate noise. There exists a deterministic \(\gamma > 0\), independent of \(\kappa\), such that for all initial \(u_0\), and all \(\kappa \in [0,1]\) there is a random constant \(D_\kappa = D_\kappa(u_0,\omega)\) so that for all zero-mean \(g_0 \in H^1\) and all \(t>0\) the following holds almost surely \[\begin{equation} \|g_t\|_{H^{-1}} \leq D_\kappa e^{-\gamma t}\|g_0\|_{H^1}.\label{eqEM}\tag{EM} \end{equation}\] The random constant \(D_\kappa\), has finite second moment uniformly bounded in \(\kappa\).
Theorem 2 can be seen as a direct consequence of Theorem 1 and follows from a fairly straight forward argument using the mild form of \(\eqref{eqAD}\) and estimates on the stochastic convolution. This argument is carried out in Bedrossian, Blumenthal, and Punshon-Smith (2019a).
Lagrangian chaos
It has long been understood in the physics community (e.g. Bohr et al. (2005), Antonsen Jr and Ott (1991), Ott (1999), Shraiman and Siggia (2000)) that the predominant mechanism for mixing in spatially regular fluids is the chaotic motion of the particle trajectories \(x_t = \phi^t(x)\) of the Lagrangian flow map \(\phi^t : \mathbb{T}^d \to \mathbb{T}^d\) associated to the velocity field \(u_t\), defined by \[ \frac{d}{dt} \phi^t(x) = u_t(\phi^t(x)), \quad \phi^0(x) = x\in \mathbb{T}d. \] Here we characterize chaos through having a positive Lyapunov exponent \[\begin{equation} 0< \lambda_1 := \lim_{t\to \infty} \frac{1}{t}\log|D_x\phi^t| \, .\label{eqPE}\tag{PE} \end{equation}\] This property is typically referred to as Lagrangian chaos in the fluid mechanics literature.
In the deterministic setting, proving positivity of Lyapunov exponents as in \(\eqref{eqPE}\) is currently hopelessly out of reach due to the possible formation of coherent structures and lack of ergodicity. However, starting with the seminal work of Furstenberg (Furstenberg (1963)), significant success has been achieved in proving existence and positivity of Lyapunov exponents in the context of random dynamical systems (Arnold (2013), Kifer (2012), P. H. Baxendale (1989), Ledrappier and Young (1985)). Ideas in this vein are what enabled us to prove the following Lagrangian chaos result, the first step in the proof of Theorem 3.
Theorem 3 (Lagrangian chaos, Bedrossian, Blumenthal, and Punshon-Smith 2018):
Let \(u_t\) solve \(\eqref{eqSNS}\) with non-degenerate noise as above, then there exists a deterministic constant \(\lambda_1 > 0\) (independent of \(u_0\) and \(\omega\)) for which \(\eqref{eqPE}\) holds almost surely.
Decay of correlations and mixing
Let us now address how \(\eqref{eqEM}\) is obtained in the case \(\kappa = 0\). In this case, the solution \(g_t\) is given by \(g_t = g_0 \circ (\phi^t)^{-1}\). In view of this, \(\eqref{eqPE}\) suggests that \(g_t\) is `stretched out’ considerably as \(t\) increases, leading to a rapid generation of high frequencies as oppositely signed values of the concentration profile \(g_t\) ``pile up’’ against each other almost everywhere in the domain. Indeed, this local-to-global mechanism is widely used in dynamics. It is known as decay of correlations and takes the form \[\begin{equation} \left|\int (f\circ \phi^t)\, g dx \right| \leq D_\kappa e^{-\gamma t}\|f\|_{H^1}\|g\|_{H^1}\label{eq1}\tag{1} \end{equation}\] for each mean zero \(f,g\in H^1\) and \(t>0\). This is equivalent to exponential mixing \(\eqref{eqEM}\).
Despite this simple picture, passing from \(\eqref{eqPE}\) to \(\eqref{eq1}\) requires serious work. When random driving is present, the two-point process is a powerful tool for proving exponential correlation decay (P. Baxendale and Stroock (1988), Dolgopyat et al. (2004)).
In our context, this is the Markov process that simultaneously tracks two particles subjected to the same velocity field \((u_t,\phi^t(x),\phi^t(y))\) for \(x \neq y\). Correlation decay for generic noise realizations is connected with the rate at which the probabilistic law of \((u_t, \phi^t(x), \phi^t(y))\) relaxes to its equilibrium statistics (known as geometric ergodicity).
The proof of Theorem 2 with \(\kappa = 0\) utilizes this connection using tools from the theory of Markov chains, particularly the Harris theorem Meyn and Tweedie (2012). The main difficulty to overcome here is the degeneracy in the \((u_t, \phi^t(x), \phi^t(y))\) process near the diagonal \(\{x=y\}\). One needs to show that any time two particles are close, they separate again exponentially fast. This effectively amounts to a large deviation estimate on the convergence of finite-time Lyapunov exponents to the asymptotic Lyapunov exponent deduced in Theorem 3, and is carried out in Bedrossian, Blumenthal, and Punshon-Smith (2019b).
It remains to incorporate molecular diffusion (\(\kappa > 0\)) into this scheme. This comes down again to the two-point process, now with Lagrangian flow \(\phi^t_\kappa\) augmented by an additional white noise term with variance \(\sqrt{\kappa}\) to account for molecular diffusivity. The primary step is to show that one can pass to the singular limit \(\kappa \to 0\) in the dominant eigenvalue, eigenfunction pair for the Perron-Frobenius operator corresponding to \((u_t, \phi^t_\kappa(x), \phi^t_\kappa(y))\); this is carried out in Bedrossian, Blumenthal, and Punshon-Smith (2021).