Abstract
The mixture cure model in survival analysis has received large and growing attention in the last few decades. Here we present an overview drawing together early results and some recent new developments, and pointing out areas where further work is needed.
Introduction: the Mixture Cure Model
In certain clinical trials or observational studies, either prospective or based on historically accumulated data, individuals are or have been followed up for a period of time and their status at some endpoint reported. See for example the National Cancer Institute (2019) (Surveillance, Epidemiology, and End Results, US National Cancer Institute) data base, which contains a massive amount of data with extended followup on a wide range of cancers — an important source for historical data. In another context, in Liu et al. (2018), the times of occurrence of four endpoints (overall survival, disease-specific survival, disease-free interval, or progression-free interval) for 11,160 patients across 33 cancer types were obtained from follow-up data files, with a view to making recommendations to clinicians regarding their patient’s status.
The data confronting the statistician consists of observations like this, on the time to the occurrence of some event such as death, or the recurrence of a disease, etc. For definiteness, suppose we are analysing overall survival, and the measurement is the life-lengths of a sample of individuals. A particular characteristic of this kind of data is that it is commonly right-censored. This happens when an individual’s complete lifetime is not observed, either because s/he left the study early for some reason, or was still alive at the end of the study (and all real-life studies must be terminated at some finite time). The censored observations must be taken into account in any analysis; to ignore them would introduce bias, in that, typically, some of the longer lifetimes would have been ignored.
Methods for the analysis of such survival data have long been known. See for example Kalbfleisch and Prentice (1981). A good place to start is simply to look at the data, literally, in the form of the Kaplan-Meier Estimator (KME, Kaplan and Meier (1958)), which is a nonparametric estimator of the survival function (the tail, or complement, of the distribution describing the lifetimes) which takes into account the censoring. An example KME plot is the first thing we see when looking at the current Wikipedia entry for the KME.
Notable about this example and many others we can see in the literature is that the survivor function is improper; it does not reach zero at its right endpoint. Equivalently, in such cases, the KME as a cdf has total mass less than 1. This is so for all of the data sets in Liu et al. (2018), and we give other examples below.
A KME which levels off or “plateaus” at its right hand end because the largest or perhaps a number of the largest lifetimes are censored may indicate the presence of a proportion of individuals in the population who will not suffer the event, no matter how long they are followed up. We refer to them as “cured of” or “immune to” the event, and methods are now well developed to deal with this kind of data, generally known as cure model methods. As well as providing significant extra information beyond that of a standard survival analysis, ignoring the presence of cures in an analysis can lead to biased and misleading conclusions, sometimes with profound consequences for diagnostic prognostications and evaluations. Various versions of cure models have been formulated over the years but here we concentrate on a version which seems easiest to us to formulate, analyse and interpret: the mixture cure models.
Boag’s Data
The first recognition of the need for and implementation of a cure model seems to have been by Boag (1949). He collected data from a number of centres in England, for various sites of the disease and treatment methods, and noticed that, while the distributions of life-lengths (measured from the beginning of treatment) of those dying appeared to follow quite well a lognormal distribution, “a large group of patients … were still alive and symptom-free (at the limits of his followup). In this instance we should conclude that a proportion of the patients was permanently cured by the treatment”.
Accordingly, he proposed a model in which “A proportion, \(c\), of all patients treated is permanently cured. Patients in the remaining fraction \((1- c)\) are liable to die of cancer if they do not previously die from other causes.” He went on to fit by maximum likelihood a lognormal distribution with mass at infinity – a mixture cure model – to followup data on 121 women with breast cancer, finding a significant “cured” proportion in the data.
Fig. 2.1 shows the KME of the survival distribution with 95% confidence intervals, and a Weibull mixture distribution fitted, for Boag’s 121 breast cancer patients. The KME jumps only at uncensored (death) times, remaining constant at censored times. For this data it clearly levels off at a value less than 1, consistent with Boag’s observation of a possible cured component, with a tendency to remain constant at lifetimes greater than 90 months, except for one late death at 120.6 months. The length of the level stretch at the righthand end of the KME is indicative of the amount of followup in the data.
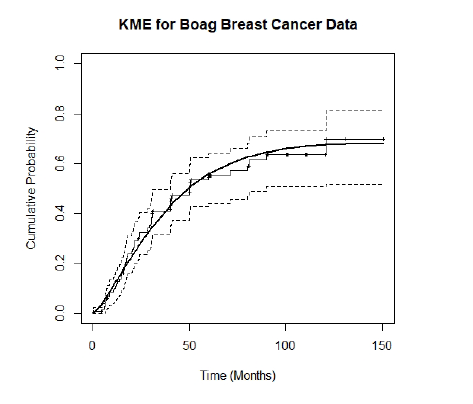
Figure 2.1: KME for Boag Breast Cancer Data with Fitted Weibull Mixture Distribution.
The KME in Fig. 2.1 is very typical of the kind that can be seen in much of the medical literature. It displays clearly the main issues we want to address:
\(\bullet\) has the KME levelled off at a value significantly less than 1 thereby indicating the possible presence of immunes in the population? and
\(\bullet\) has the KME levelled off sufficiently for us to be confident of this?
Since the prospect of a cure is surely the hope of many or most medical procedures, the importance of Boag’s insight can hardly be overstated. Following his groundbreaking paper a number of researchers followed up with various aspects and analyses of the model, but the first systematic treatment of what is now called the long term survivor or cure mixture model seems to have been in Maller and Zhou (1996). That book combines nonparametric and parametric theoretical formulations and proofs with many practical applications and examples of the model.
There has been an upsurge in interest in the model since the 1990s, with many applications areas explored, especially in medical statistics, and some substantial theoretical advances made. Correspondingly, computational facilities have improved tremendously, and with modern capabilities a wide variety of parametric models of censored data with long term survivors can now be fitted routinely with the statistical package R.
More recent work of the present authors concerns some aspects left unresolved in Maller and Zhou (1996), as well as some quite new points of view, which we discuss below.
Notation, Assumptions and Distributions
A tractable and reasonably realistic model for the data is an independent and identically distributed (iid) censoring model with right censoring. In it, a sample of size \(n\) consists of observations on the sequence of iid 2-vectors \(\big(T_i=T_i^*\wedge U_i, C_i={\bf 1}(T_i^*\le U_i);\, 1\le i\le n\big)\) where the \(T_i\) represent the censored survival times and the \(C_i\) are the censor indicators. The \(T_i^*\) with continuous cumulative distribution function (cdf) \(F^*\) on \([0,\infty)\) represent the times of occurrence of the event under study. The \(U_i\), iid with continuous cdf \(G\) on \([0,\infty)\), are censoring random variables, independent of the \(T_i^*\). In a sample from a population containing long-term survivors we observe the censored random variables \(T_i=T_i^*\wedge U_i\), these being potential lifetimes censored at a limit of follow-up represented for individual \(i\) by the random variable \(U_i\) with censor indicators \(C_i={\bf 1}(T_i^*\le U_i)\).
In the general mixture cure model, the censoring distribution \(G\) of the \(U_i\) is always assumed proper (total mass 1), but the distribution \(F^*\) of the \(T_i^*\) may be improper, with mass \(1-p\), \(0\le p<1\), at infinity. We assume \(F^*\)to be of the form \[\begin{equation} \label{FandF0} F^*(t)=pF(t), \end{equation}\] where \(0<p\le 1\) and \(F\) is a proper distribution. \(F\) is the distribution of the lifetimes of susceptible individuals in the population; only these can experience the event of interest and have a potentially uncensored failure time. The remainder are immune to the event of interest or cured of it. The presence of cured subjects is signalled by a value of \(p<1\), in which case the distribution \(F^*\) is improper, with total mass \(p\). Then \(1-p\) is the proportion of immune or cured individuals in the population.
We do not know whether a particular censored lifetime in the sample is from a cured or immune individual (uncensored lifetimes are obviously not from immunes); but observations on cured or immune individuals are always censored; those on susceptibles may or may not be according as the corresponding \(T_i^*>U_i\) or not.
Data Display: the Kaplan-Meier Estimator
The KME is a highly informative data display which shows clearly in visual form the features we want to investigate. To define it, denote the ordered sample lifetimes as \(T_n^{(1)}< T_n^{(2)}< \cdots <T_n^{(n)}\), with associated censor indicators \(C_n^{(1)}, C_n^{(2)}, \ldots, C_n^{(n)}\). Let \(M(n)=T_n^{(n)}=\max_{1\leq i\leq n}T_i\) be the largest survival time and let \(M_u(n)\) be the largest observed uncensored survival time. An explicit definition of the KME is \[ F_n(t):= 1-\prod_{1\le i\le n: \, T_n^{(i)} \le t}^n \big(1- \frac{C_n^{(i)}}{n-i+1} \big), \ {\rm for}\ 0<t\le M(n), \]
with \(\hat F_n(0):=0\) and \(\hat F_n(t):=\hat F_n(M(n))\) for \(t> M(n)\). In (4.1), \(n-i+1\) is the number of subjects “at risk” at times just prior to \(T_n^{(i)}\). Recall we assume \(F^*\) and \(G\) are continuous so there are no tied survival times in the data with probability 1. Let \(\hat p_n:= \hat F_n(M(n))\) be the value of the KME at its right extreme.
In a sample we observe data values \((t_i, c_i)_{1\le i\le n}\) for \((T_i,C_i)_{1\le i\le n}\), order them as \(t_n^{(1)}< t_n^{(2)}< \cdots <t_n^{(n)}\), and define associated censor indicators \(c_n^{(1)}, c_n^{(2)}, \ldots, c_n^{(n)}\). Then \(t_n^{(n)}=\max_{1\leq i\leq n}t_i\) is the largest observed survival time. The sample KME is the same function with observed data values substituted for the random quantities, and we obtain a sample estimate of \(\hat p_n\) by substituting \(t_n^{(n)}\) for \(M(n)\).
A nonparametric estimate of the population proportion dying is given by the maximum value of the KME, that is \(\hat p_n\), and its complement is the estimated cure proportion, which as can be seen in Fig. 2.1 for Boag’s data is 0.30 with a 95% confidence interval (CI) of \([0.19, 0.48]\). This interval excludes 0, in general agreement with Boag’s observation of a possible cured component. This confidence interval assessment though indicative is not strictly correct usage, however, as the restriction of \(p\) to \([0,1]\) should be taken into account, as should the fact that \(\hat p_n\) is calculated from the KME at a random (not deterministic) time.
When a parametric mixture model such as the Weibull is fitted, a rigorous test for \(H_0: p=1\) (no immunes present) is available (see Section 5.3, p.109, of Maller and Zhou (1996)), and a nonparametric test using \(\hat p_n\) is outlined in Section 4.2, p.76, p.109, of Maller and Zhou (1996) (with percentage points in Table A.1 of the book), but we still do not have complete understanding of the distribution of \(\hat p_n\) under the null hypothesis \(H_0\).
The KME contains further evidence about the existence of a cured component. We see in Fig.2.1 a tendency for the KME to remain constant at lifetimes greater than 90 months, except for one late death at 120.6 months. The length of the level stretch at the righthand end of the KME is indicative of the amount of followup in the data. A statistic \(Q_n\) is suggested in Maller and Zhou (1996) for assessing “sufficient followup”.
Recent Research
These ideas are related to the magnitudes of the largest survival time observed, and the largest uncensored survival time observed, and the numbers of observations in the two time intervals defined by these. A key structural result obtained in Maller, Resnick, and Shemehsavar (2020) is that, conditional on the value of the largest uncensored survival time, and knowing the number of censored observations exceeding this time, the sample partitions into two independent subsamples, each subsample having the distribution of an iid sample of censored survival times, of reduced size, from truncated random variables. This result provides valuable insight and intuition into the construction of samples of censored survival data, and facilitates the calculation of explicit finite sample formulae, for example, for the joint distribution of the largest and the largest uncensored survival time observed, and for \(Q_n\). Further, the asymptotic distributions of these statistics can then be worked out under conditions related to those familiar from extreme value theory. Our recent research is very much in this line. See Escobar-Bach et al. (2020) (adjusting for insufficient follow-up), Maller and Resnick (2020) (extremes of censored and uncensored lifetimes), Maller, Resnick, and Shemehsavar (2020) (splitting the sample at the largest uncensored observation, testing for sufficient followup, estimating the probability of being cured).
Conclusion: Take-Away Points
\(\bullet\) It’s very common in survival analysis to encounter a KME which has levelled off at a value less than 1. This may indicate the presence of immune or cured individuals in the population — but not always — even in the absence of cures, it’s possible for the right extreme of the KME to be less than 1 just by chance.
\(\bullet\) A significance test is available for the hypothesis \(H_0: p=1\) when a well-fitting parametric model has been found for the data. A wide variety of models can be fitted routinely with R. These cover a class of generalised F models and, as a submodel, an extended generalised gamma model, which between them include as submodels most of the usual survival distributions such as the exponential, Weibull, lognormal, Gumbel, log-logistic, Burr, etc.
\(\bullet\) A nonparametric test for \(H_0: p=1\) is available too, but at present we have to rely on simulated, tabulated, percentage points for the distribution.
\(\bullet\) An important point is whether the KME has levelled off sufficiently at its right endpoint. The \(Q_n\) statistic has been developed to measure and test for this.
\(\bullet\) We’ve confined our discussion to the one-sample case. In practice, we usually have one or more groups (treatment groups, or otherwise), and/or covariates, and want to examine the effects of these. Much of Maller and Zhou (1996) is concerned with methods for handling this.
\(\bullet\) We’ve also confined our discussion to medical data and survival analysis. But the methodology applies to many other kinds of time-to-event data. A wide variety of examples can be found in a web search. Maller and Zhou (1996) use much criminological data (time to re-arrest of a released prisoner, etc.) to illustrate the methods.
\(\bullet\) Ignoring the possible presence of cured, immune or long-term survivors in a population not only risks losing valuable information but can result in bias and misleading conclusions. An important point is that including the possibility of long-term survivors in any survival analysis can do no damage; if their presence is allowed for but found not to be significant, no harm is done (but keeping in mind the risks of overfitting).
\(\bullet\) The mixture cure model can be regarded as a special case of a competing risks analysis where death or failure of an individual may be due to a number of possible causes. The issue of sufficient followup is clearly relevant in this context, but has not been addressed at all, to our knowledge.