Abstract
It is increasingly common for data to be collected adaptively, where experimental costs are reduced progressively by assigning promising treatments more frequently. However, adaptivity also poses great challenges on post-experiment inference, since observations are dependent, and standard estimates can be skewed and heavy-tailed. We propose a treatment-effect estimator that is consistent and asymptotically normal, allowing for constructing frequentist confidence intervals and testing hypotheses.
Introduction
Adaptive data collection can optimize sample efficiency during the course of the experiment for particular objectives, such as identifying the best treatment (D. Russo 2020) or improving operational performance (Agrawal and Goyal 2013) . To achieve these efficiency gains, the experimenter—rather than staying with a fixed randomization rule—updates the data-collection policy (which maps individual characteristics/contexts to treatments/actions) in response to observed outcomes over the course of the experiment. In this way, the experimenter can resolve uncertainty about some aspects of the data generating process at the expense of learning little about others (Murphy 2005). A common family of the design algorithms are bandit algorithms (Lai and Robbins 1985), where treatment assignments are selected to trade off exploration and exploitation to maximize the cumulative performance over time.
The increasing popularity of adaptive experiments results in the growing availability of data collected from such designs. A natural query arises: can we reuse the data to answer a variety of questions that may not be originally targeted by the experiments? However, adaptivity also poses great statistical challenges if the post-experiment objective differs significantly from the original, and standard approaches used to analyze independently collected data can be plagued by bias, excessive variance, or both. This post seeks to address the problem of offline policy evaluation, which is to estimate the expected benefit of one treatment assignment policy—often termed as policy value—with data that was collected using another potentially different policy. For example, in personalized healthcare, doctors may use electronic medical records to evaluate how particular groups of patients will respond to heterogenenous treatments (e.g., different types of drugs/therapies or different dosage levels of the same drug) (Bertsimas et al. 2017), whereas in targeted advertising, retailers may want to understand how alternative product promotions (either in mail or online) affect different consumer segments (Schnabel et al. 2016).
Problem formulation
Consider that samples are collected by a multi-armed bandit algorithm, where each observation is represented by a tuple \((W_t, Y_t)\). The random variables \(W_t \in \{1, 2, \dots, K\}\) are called the arms, treatments or interventions. The reward or outcome \(Y_t\) represents the individual’s response to the treatment, for which we use the potential outcome framework and denote \(Y_t(w)\) as the random variable representing the outcome that would be observed if individual \(t\) were assigned to a treatment \(w\). We here consider a stationary setting of the potential outcomes, where \((Y_t(1),Y_t(2),\dots, Y_t(K))\) is sampled from a fixed distribution. The set of observations up to a certain time \(H_t := \{(W_s, Y_s) \}_{s=1}^T\) is called a history. The treatment assignment probabilities (also known as propensities) \(e_t(w) := \mathbb{P}[W_t = w | H_{t-1}]\) are updated over time by the experimenter, in response to the observations \(H_{t-1}\).
Our goal is to estimate the value of an arm \(w\), denoted by \(Q(w):=\mathbb{E}[Y_t(w)]\). We will provide consistent and asymptotically normal test statistics for \(Q(w)\), so that we can construct confidence intervals around the estimations to test hypotheses. We would like to do that even in data-poor situations in which the experimenter did not collect many samples around the arm \(w\).
Our approach
The main challenging in evaluating an arm \(w\) with observational data is known as the overlap issue between the target arm and the data-collection mechanism, when the arm assignments made during data collection differ substantially from the target arm \(w\). This issue becomes more severe when data is collected adaptively, since overlap with the target arm can deteriorate as the experimenter shifts the data-collection mechanism in response to what they observe. As a result, estimates from standard estimators can be skewed and heavy-tailed.
Our approach to recover the asymptotic normality is done in three steps. First, we construct an unbiased arm evaluation score of each sample, which is a transformation of the observed outcome. Second, we average these scores with non-uniform and data-adaptive weights, obtaining a new estimator with controlled variance. Finally, by dividing the estimator by its estimated standard error we obtain a test statistic that is consistent and asymptotically normal.
Step 1: Constructing an unbiased arm evaluation score for each observation
The arm evaluation scoring rule should address the sampling bias issue, which is notorious in adaptively collected data (Nie et al. 2018). One natural method is to re-weight observed outcomes based on importance sampling, which results in an inverse propensity score weighted (IPW) estimator: \[\begin{equation} \label{eq:ipw} \widehat{Q}_T^{IPW}(w) := \frac{1}{T}\sum_{t=1}^T\widehat{\Gamma}_t^{IPW}(w), \ \mbox{where} \ \widehat{\Gamma}_t^{IPW}(w) := \frac{\mathbb{I}\{W_t=w\}}{e_t(w)} Y_t. \end{equation}\] With the observation that \(\mathbb{P}({W_t = w | H_{t-1}, \, Y_t(w)} = \mathbb{P}({W_t = w | H_{t-1}} = e(w;H_{t-1})\), one can immediately see the unbiasedness of \(\widehat{\Gamma}_t^{IPW}(w)\) that has \(\mathbb{E}[\widehat{\Gamma}_t^{IPW}(w)|H_{t-1}]=Q(w)\).
The augmented inverse propensity weighted (AIPW) estimator generalizes the above by incorporating regression adjustment : \[\begin{equation} \label{eq:aipw} \begin{split} &\widehat{Q}_T^{AIPW}(w) := \frac{1}{T}\sum_{t=1}^T \widehat{\Gamma}_t^{AIPW}(w), \ \mbox{where}\ \widehat{\Gamma}_t^{AIPW}(w) := \hat{\mu}_t(w) + \frac{\mathbb{I}\{W_t=w\}}{e_t(w)} \left( Y_t - \hat{\mu}_t(w)\right). \end{split} \end{equation}\] The symbol \(\hat{\mu}_t(w)\) denotes an estimator of the conditional mean function \(\mu(w) = \mathbb{E}[Y_t(w)]\) based on the history \(H_{t-1}\), but it need not be a good one—it could be biased or even inconsistent. The second term of \(Y_t - \hat{\mu}_t(w)\) acts as a bias-correction term: adding it preserves unbiasedness but also reduces the variance, since the residual—when \(\hat{\mu}_t(w)\) is a reasonable estimator of \(\mu(w)\)—potentially has a smaller absolute mean as compared to the raw outcome \(Y_t\). We will hereby use the AIPW score \(\widehat{\Gamma}_t^{AIPW}(w)\) for each observation \(t\).
Step 2: Averaging arm evaluations with adaptive weights
When data is collected non-adaptively but by a fixed randomization rule, AIPW estimator is semiparametrically efficient (Hahn 1998). However, adaptivity makes the sampling distribution non-normal and heavy-tailed, and the variance of the AIPW scores \(\widehat{\Gamma}_t^{AIPW}(w)\) can vary hugely over the course of experiment. In fact, the conditional variances \(\mbox{Var}(\widehat{\Gamma}_t^{AIPW}(w)|H_{t-1})\) depend primarily on the behavior of the inverse propensities \(1/e_t(w)\), which may explode to infinity or fail to converge.
To address this difficulty, we consider a generalization of the AIPW estimator, which non-uniformly averages the unbiased scores \(\widehat{\Gamma}^{AIPW}_t(w)\) using a sequence of adaptive weights \(h_t(w)\). The resulting estimator is the adaptively-weighted AIPW estimator: \[\begin{align} \label{eq:aw} \widehat{Q}^{h}_T(w) = \frac{\sum_{t=1}^T h_t(w) \widehat{\Gamma}_t^{AIPW}(w)}{\sum_{t=1}^T h_t(w)}. \end{align}\]
Adaptive weights \(h_t(w)\) provide an additional degree of flexibility in controlling the variance and the tail of the sampling distribution. When chosen appropriately, these weights compensate for erratic trajectories of the assignment probabilities \(e_t(w)\), stabilizing the variance of the estimator. A natural choice of adaptive weights is to approximate the inverse standard deviation of the \(\widehat{\Gamma}_t^{AIPW}(w)\). In this way each re-weighted term \(h_t\widehat{\Gamma}_t^{AIPW}(w)\) has comparable variance, such that averaging these object may lead to a normal limiting distribution. We shall refer it to constant-allocation weighting scheme since each weighted element \(h_t\widehat{\Gamma}_t^{AIPW}(w)\) contributes to roughly the same share of variance in the final estimator. Weights of this type were proposed by Luedtke and Laan (2016) for the purpose of estimating the expected value of non-unique optimal policies that possibly depend on observable covariates.
More generally, to get an adaptively-weighted AIPW estimator \(\widehat{Q}^{h}_T(w)\) that is consistent and asymptotically normal, we require the following assumptions on our weighting schemes stated below.
Assumption 1 (Infinite sampling). \(\big(\sum_{t=1}^T h_t(w)]\big)^2 \,\big/\, \mathbb{E}\big[ \sum_{t=1}^T \frac{h^2_t(w)}{e_t(w)} \big] \xrightarrow[T \to \infty]{p} \infty.\)
Assumption 2 (Variance convergence). \(\sum_{t=1}^T \frac{h^2_t(w)}{e_t(w) } \,\bigg/\, \mathbb{E}\big[ \sum_{t=1}^T \frac{h^2_t(w)}{e_t(w)} \big]\xrightarrow[T \to \infty]{L_p} 1\), for some \(p>0\).
Assumption 3 (Bounded moments). \(\sum_{t=1}^T \frac{h^{2 + \delta}(w)}{e^{1 + \delta}(w) } \,\Big/\, \mathbb{E}\Big[ \Big(\sum_{t=1}^T \frac{h^2_t(w)}{e_t(w)} \Big)^{1 +\delta/2}\Big]\xrightarrow[T \to \infty]{p} 0\), for some \(\delta>0\).
Above, Assumption 1 requires that the effective sample size after adaptive weighting goes to infinity, which implies that the estimator converges. Assumption 3 is a Lyapunov-type regularity condition on the weights, which controls higher moments of the distribution. Assumption 2 is the more subtle condition that standard estimators such as AIPW estimator (i.e., \(h_t(w) \equiv 1\)) often fail to satisfy. We refer interesting readers to our paper Hadad et al. (2021) for a recipe on building weights that satisfy Assumption 2. In particular, we note a two-point allocation weighting scheme when the assignment probabilities \(e_t\) reflect the experimenter’s belief on arm optimality (as is the case for Thompson sampling). This weighting scheme allows us to downweight samples with small propensities more boldly but still preserve the asymptotic normality, and therefore often merits smaller variance and tighter confidence intervals as compared to the constant-allocation scheme.
Step 3: Estimating standard error and constructing a test statistic
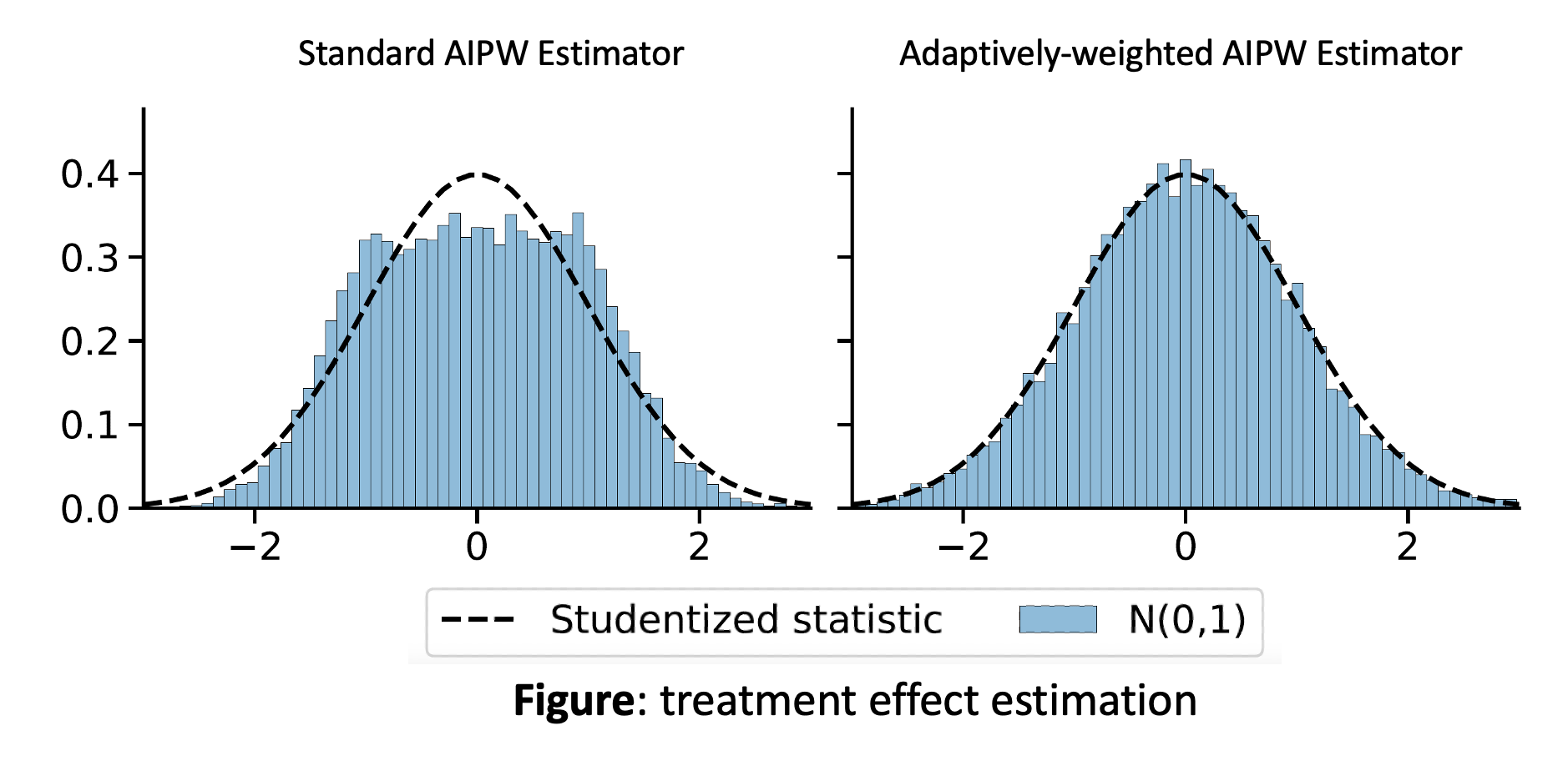
With the evaluation weights discussed in step 2, when normalized by an estimate of its standard deviation, the adaptively-weighted AIPW estimator has a centered and normal asymptotic distribution. Similar ``self-normalization’’ schemes are often key to martingale central limit theorems (Peña, Lai, and Shao 2008).
Theorem. Suppose that we observe arms \(W_t\) and rewards \(Y_t=Y_t(W_t)\), and that the underlying potential outcomes \((Y_t(w))_{w \in \mathcal{W}}\) are independent and identically distributed with nonzero variance, and satisfy \(\mathbb{E}|Y_{t}(w)|^{2+\delta} < \infty\) for some \(\delta > 0\) and all \(w\). Suppose that the assignment probabilities \(e_t(w)\) are strictly positive and let \(\hat{\mu}_t(w)\) be any history-adapted estimator of \(Q(w)\) that is bounded and that converges almost-surely to some constant \(\mu_{\infty}(w)\). Let \(h_t(w)\) be non-negative history-adapted weights satisfying Assumptions 1-3. Suppose that either \(\hat{\mu}_t(w)\) is consistent or \(e_t(w)\) has a limit \(e_{\infty}(w) \in [0, \, 1]\), i.e., either \[\begin{equation} \label{eq:e_mu_alternative} \hat{\mu}_t(w) \xrightarrow[t \to \infty]{a.s.} Q(w) \quad \text{or} \quad e_t(w) \xrightarrow[t \to \infty]{a.s.} e_{\infty}(w) \end{equation}\] Then, for any arm \(w \in \mathcal{W}\), the adaptively-weighted estimator \(\widehat{Q}_T^{h}(w)\) is consistent for the arm value \(Q(w)\), and the following studentized statistic is asymptotically normal: \[\begin{equation} \begin{aligned} \label{eq:clt} &\frac{\widehat{Q}_T^{h}(w) - Q(w)}{\widehat{V}_T^{h}(w)^{\frac{1}{2}}} \xrightarrow{d} \mathcal{N}(0, 1), \ \ \ \text{where} \ \widehat{V}_T^{h}(w) := \frac{\sum_{t=1}^T h^2_t(w) \left( \widehat{\Gamma}_t(w) - \widehat{Q}_T(w) \right)^2}{\left( \sum_{t=1}^T h_t(w) \right)^2}. \end{aligned} \end{equation}\]
Simulations
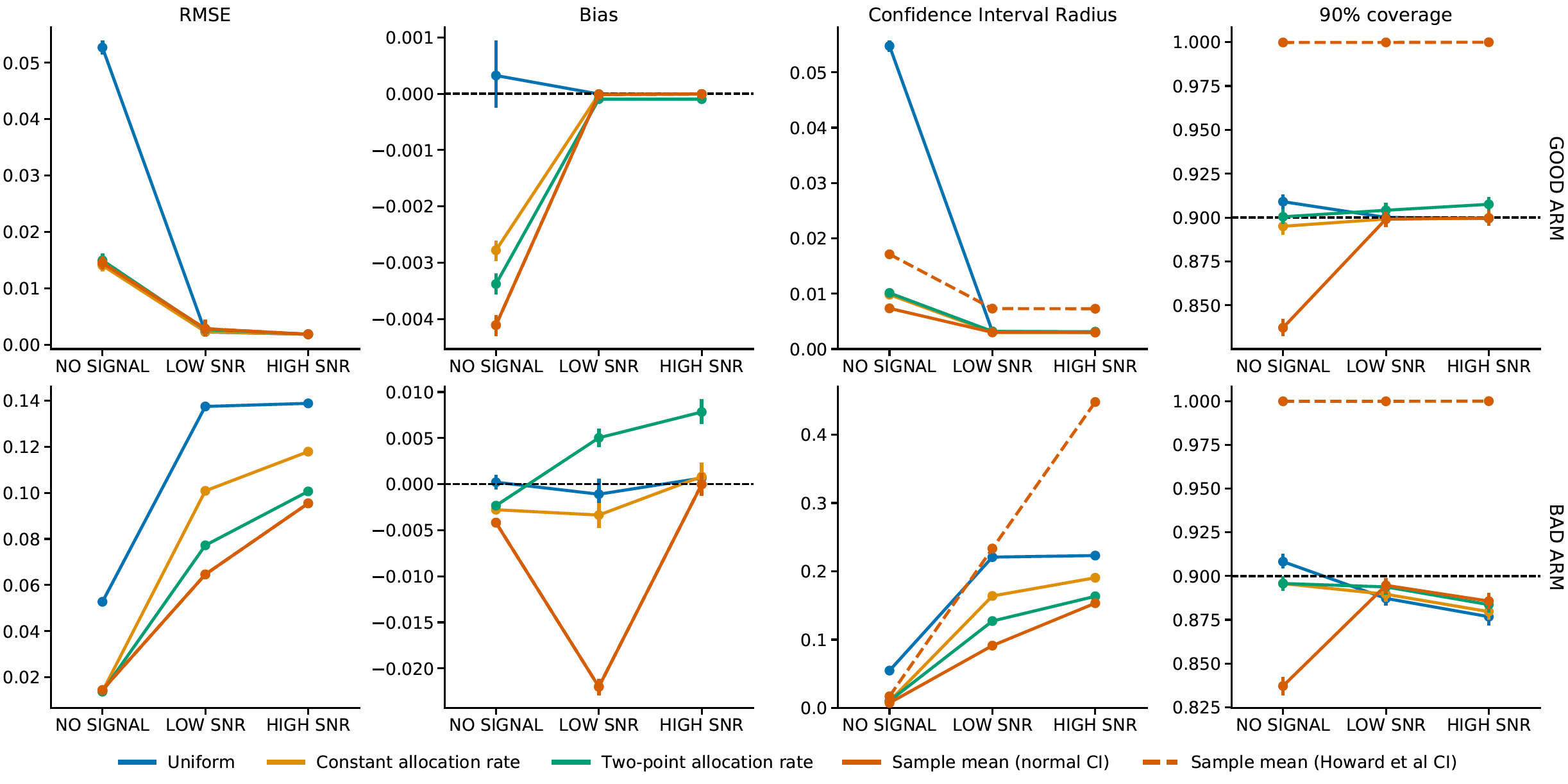
We consider three simulation settings, each with \(K = 3\) arms that yield rewards observed with additive \(\text{uniform}[-1, 1]\) noise. The settings vary in the difference between the arm values. In the no-signal case, we set arm values to \(Q(w) = 1\) for all \(w \in \{1, 2, 3\}\); in the low signal case, we set \(Q(w) = 0.9+ 0.1w\); and high signal case we set \(Q(w) = 0.5 + 0.5w\). During the experiment, treatment is assigned by a modified Thompson sampling method: first, tentative assignment probabilities are computed via Thompson sampling with normal likelihood and normal prior(D. J. Russo et al. 2018); they are then adjusted to impose the lower bound \(e_t(w) \geq (1/K)t^{-0.7}\).
We show comparison among four point estimators of arm values \(Q(w)\): the sample mean, the AIPW estimator with uniform weights (labeled as “unweighted AIPW”), and the adaptively-weighted AIPW estimator with constant and two-point allocation schemes. For the AIPW-based estimators, we use the same formula given in our theorem to construct confidence intervals. For the sample mean we use the usual variance estimate \(\smash{\widehat{V}^{AVG}(w) := T_w^{-2} \sum_{t: W_t = w}^{T} (Y_t - \widehat{Q}^{AVG}_T(w))^2}\). Approximate normality is not theoretically justified for the unweighted AIPW estimator or for the sample mean. We also consider non-asymptotic confidence intervals for the sample mean, based on the method of time-uniform confidence sequences described in Howard et al. (2021). We refer interesting readers to our paper for more results on estimating other arms as well as the contrast between arms (Hadad et al. 2021 ).
The below panel demonstrates that we are able to estimate the “good” arm value \(Q(3)\) with considerable ease in high- and low-signal settings, in that all methods produce point estimates with negligible bias and small root mean-squared error, and moreover attain roughly correct coverage for large \(T\). Conversely, estimating the “bad” arm value \(Q(1)\) is challenging. Although the AIPW estimator is unbiased, it performs very poorly in terms of RMSE and confidence interval width. In the low and high signal case, its problem is that it does not take into account the fact that the bad arm is undersampled, so its variance is high. Of our two adaptively-weighted AIPW estimators, two-point allocation better controls the variance of bad arm estimates by more aggressively downweighting `unlikely’ observations associated with large inverse propensity weights; this results in smaller RMSE and tighter confidence intervals. For the sample-mean estimator, naive confidence intervals based on the normal approximation are invalid, with severe under-coverage when there’s little or no signal. On the other hand, the non-asymptotic confidence sequences of Howard et al. (2021) are conservative and often wide.
Extensions
One direct extension is to apply the above adaptive weighting technique to evaluating policies on populations with hetegeneous outcomes, using data that is collected adaptively via contextual bandit algorithms. In Zhan, Hadad, et al. (2021), we carefully choose adaptive weights to accommodate the variances of AIPW scores that may differ not only over time but also across the context space. The resulting estimator further reduces estimation variance.
Aside from policy evaluation, learning the optimal treatment assignment policies using adaptive data is also desirable, which enables personalized decision making in a wide variety of domains. In Zhan, Ren, et al. (2021), we establish the first-of-the-kind regret lower bound that characterizes the fundamental difficulty of policy learning with adaptive data. We then propose an algorithm based on re-weighted AIPW estimators and show that it is minimax optimal with the best weighting scheme.