Introduction
A NHPP defined on \({\cal S} \subset \mathbb{R}^{d}\) can be fully characterized through its intensity function \(\lambda: {\cal S} \rightarrow [0, \infty)\). We present a general model for the intensity function of a non-homogeneous Poisson process using measure transport. The model finds its roots in transportation of probability measure (Marzouk et al. 2016), an approach that has gained popularity recently for its ability to model arbitrary probability density functions. The basic idea of this approach is to construct a “transport map” between the complex, unknown, intensity function of interest, and a simpler, known, reference intensity function.
Background
Measure Transport. Consider two probability measures \(\mu_0(\cdot)\) and \(\mu_1(\cdot)\) defined on \({\cal X}\) and \({\cal Z}\), respectively. A transport map \(T: {\cal X} \rightarrow {\cal Z}\) is said to push forward \(\mu_0(\cdot)\) to \(\mu_1(\cdot)\) (written compactly as \(T_{\#\mu_0}(\cdot) = \mu_1(\cdot)\)) if and only if \[\begin{eqnarray} \label{transport_map} \mu_1(B) = \mu_0(T^{-1}(B)), \quad \mbox{for any Borel subset } B \subset {\cal Z}. \end{eqnarray}\]
Suppose \({\cal X}, {\cal Z} \subseteq \mathbb{R}^{d}\), and that both \(\mu_0(\cdot)\) and \(\mu_1(\cdot)\) are absolutely continuous with respect to the Lebesgue measure on \(\mathbb{R}^{d}\), with densities \(d\mu_0(x) = f_0(x) d x\) and \(d\mu_1(z) = f_1(z) d z\), respectively. Furthermore, assume that the map \(T(\cdot)\) is bijective differentiable with a differentiable inverse \(T^{-1}(\cdot)\) (i.e., assume that \(T(\cdot)\) is a \(C^{1}\) diffeomorphism), then we have \[\begin{equation} \label{eq:transport} f_0(x) = f_1(T(x)) \|\mbox{det}(\nabla T(x))\|, \quad x \in {\cal X}. \end{equation}\]
Triangular Map. One particular type of transport map is an , that is, \[\begin{eqnarray} \label{triangular_map} T(x) = (T^{(1)}(x^{(1)}), T^{(2)}(x^{(1)}, x^{(2)}), \ldots, T^{(d)}(x^{(1)}, \ldots, x^{(d)}))',\quad x \in {\cal X}, \end{eqnarray}\] where, for \(k = 1,\dots, d,\) one has that \(T^{(k)}(x^{(1)}, \ldots, x^{(k)})\) is monotonically increasing in \(x^{(k)}\). In particular, the Jacobian matrix of an increasing triangular map, if it exists, is triangular with positive entries on its diagonal.
Various approaches to parameterize an increasing triangular map have been proposed (see, for example, Germain et al. (2015), Dinh, Krueger, and Bengio (2015) and Dinh, Sohl-Dickstein, and Bengio (2017)). One class of parameterizations is based on the so-called “conditional networks” (Papamakarios, Pavlakou, and Murray (2017) and Huang et al. (2018)): \[\begin{eqnarray} T_1^{(1)}(x^{(1)}) &=& S_1^{(1)}(x^{(1)}; \theta_{11}), \nonumber \\ T_1^{(k)}(x^{(1)}, \ldots, x^{(k)}) &=& S_1^{(k)}( x^{(k)}; \theta_{1k}(x^{(1)}, \ldots, x^{(k-1)}; \vartheta_{1k}) ), \quad k = 2,\dots,d, \end{eqnarray}\] for \(x \in {\cal X}\), where \(\theta_{1k}(x^{(1)}, \ldots, x^{(k-1)}; \vartheta_{1k}), k = 2,\dots,d\) is the \(k\)th “conditional network” that takes \(x^{(1)}, \ldots, x^{(k-1)}\) as inputs and is parameterized by \(\vartheta_{1k}\), and \(S_1^{(k)}(\cdot)\) is generally a very simple univariate function of \(x^{(k)}\), but with parameters that depend in a relatively complex manner on \(x^{(1)}, \ldots, x^{(k-1)}\) through the network. The class of neural autoregressive flows, proposed by Huang et al. (2018), offers more flexibility where the \(k\)-th component of the map has the form \[\begin{eqnarray} \label{uni_flow} S_1^{(k)}( x^{(k)}; \theta_{1k} ) = \sigma^{-1} \Big( \sum_{i=1}^{M} w_{1ki} \sigma( a_{1ki} x^{(k)} + b_{1ki}) \Big), \end{eqnarray}\] where \(\sigma^{-1}(\cdot)\) is the logit function, and \(w_{1ki}\) is subject to the constraint \(\sum_{i=1}^{M} w_{1ki} = 1\).
Composition of Increasing Triangular Maps. Composition of Increasing Triangular Mapsn does not break the required bijectivity of \(T(\cdot)\), since a bijective function of a bijective function is itself bijective. Computations also remain tractable, since the determinant of the gradient of the composition is simply the product of the determinants of the individual gradients. Specifically, consider two increasing triangular maps \(T_1(\cdot)\) and \(T_2(\cdot)\), each constructed using the neural network approach described above. The composition \(T_2 \circ T_1 (\cdot)\) is bijective, and its gradient at some \(x \in \cal X\) has determinant, \[ \mbox{det}(\nabla T_2 \circ T_1(x)) = (\mbox{det} (\nabla T_1(x)))(\mbox{det} (\nabla T_2(T_1(x)))).\]
Intensity Modeling and Estimation via Measure Transport
Consider a NHPP \({\cal P}\) defined on a bounded domain \({\cal X} \subset \mathbb{R}^{d}\). The density of a Poisson process with respect to the density of the unit rate Poisson process is given by \[\begin{align} f_{\lambda}(X) &= \exp(\|{\cal X}\| - \mu_{\lambda}({\cal X})) \prod_{x \in X} \lambda(x) \nonumber \\ &= \exp \Big(\int_{{\cal X}} (\lambda(x) - 1)dx + \sum_{x \in X} \log \lambda(x) \Big) \label{fdensity}. \end{align}\] where \(|B|\) denote the Lebesgue measure of a bounded set \(B \subset \mathbb{R}^{d}\), and let \(X \equiv \{x_1, \ldots, x_n\},\) where \(x_i \in {\cal X}, i = 1,\ldots,n,\) and \(n \ge 1,\) be a realization of \({\cal P}\). The unknown intensity function is estimated by a maximum likelihood approach, which is equivalent to minimizing the Kullback–Leibler (KL) divergence \(D_{KL}(p\|\|q) = \int p(x) \log (p(x)/ q(x))dx\) between the true density and the estimate: \[ \hat{\lambda}(\cdot) = \arg\min_{\rho(\cdot) \in {\cal A} }{{D_{KL}(f_{\lambda}\|f_{\rho})}} \] where \({\cal A}\) is some set of intensity functions, and \(f_\rho(\cdot)\) is the density of a NHPP with intensity function \(\rho(\cdot)\) taken with respect to the density of the unit rate Poisson process.
In order to apply the measure transport approach to intensity function estimation, we first define \(\tilde{\rho}(\cdot) = \rho(\cdot) / \mu_{\rho}({\cal X})\) and \(\tilde{\lambda}(x) = \lambda(x) / \mu_{\lambda}({\cal X}),\) so that \(\tilde{\rho}(\cdot)\) and \(\tilde{\lambda}(\cdot)\) are valid density functions with respect to Lebesgue measure. The KL divergence \(D_{KL}(f_{\lambda}\|f_{\rho})\) can be written in terms of process densities as follows, \[ D_{KL}(f_{\lambda}\|f_{\rho}) = \mu_{\rho}({\cal X)} - \mu_{\lambda}({\cal X}) \int_{{\cal X}} \tilde{\lambda}(x) \log \tilde{\rho}(x)dx - \mu_{\lambda}({\cal X}) \log \mu_{\rho}({\cal X}) + \textrm{const.}, \] where “const.” captures other terms not dependent on \(\mu_{\rho}({\cal X})\) or \(\tilde{\rho}(\cdot)\). After further approximations, we obtain the following optimization problem \[ \hat{\tilde{\lambda}}(\cdot) = \arg\min_{\tilde{\rho}(\cdot) \in {\cal \tilde{A}}} {-{\sum_{i=1}^{n} \log \tilde{\rho}(x_{i})}}, \] where now \(\tilde{\cal A}\) is some set of process densities.
We model the process density \(\tilde{\rho}(\cdot)\) using the transportation of probability measure approach. Specifically, we seek a diffeomorphism \(T: {\cal X} \rightarrow {\cal Z}\), where \({\cal Z}\) need not be the same as \({\cal X}\), such that \[ \tilde{\rho}(x) = \eta(T(x)) | \mbox{det}\nabla T(x)|, \quad x \in {\cal X},\]where \(\eta(\cdot)\) is some simple reference density on \({\cal Z}\), and \(|\mbox{det}\nabla T(\cdot)| > 0\).
We prove that the increasing triangular maps constructed using neural autoregressive flows satisfy a universal property in the context of probability density approximation.
Theorem 1. Let \(\cal P\) be a non-homogeneous Poisson process with positive continuous process density \(\tilde{\lambda}(\cdot)\) on \({\cal X} \subset \mathbb{R}^{d}\). Suppose further that the weak (Sobolev) partial derivatives of \(\tilde{\lambda}\) up to order \(d+1\) are integrable over \(\mathbb{R}^{d}\). There exists a sequence of triangular mappings \((T_i(\cdot))_{i}\) wherein the \(k\)th component of each map \(T^{(k)}_i(\cdot)\) has the form above, and wherein the corresponding conditional networks are universal approximators (e.g., feedforward neural networks with sigmoid activation functions), such that \[ \eta(T_i(\cdot)) \mbox{det} (\nabla T_i(\cdot)) \rightarrow \tilde{\lambda}(\cdot), \] with respect to the sup norm on any compact subset of \(\mathbb{R}^{d}\).
Illustration
We apply our method for intensity function estimation to an earthquake data set comprising 1000 seismic events of body-wave magnitude (MB) over 4.0. The data set is available from the package. The events we analyze are those that occurred near Fiji from 1964 onwards. The left panel of Figure 1 shows a scatter plot of locations of the observed seismic events.
We fitted our model using a composition of five triangular maps. The estimated intensity surface and the standard error surface obtained using are shown in the middle and right panels of Figure 1, respectively. The probability that the intensity function exceeds various threshold can also be estimated using non-parametric bootstrap resampling; some examples of these exceedance probability plots are shown in Figure 2.
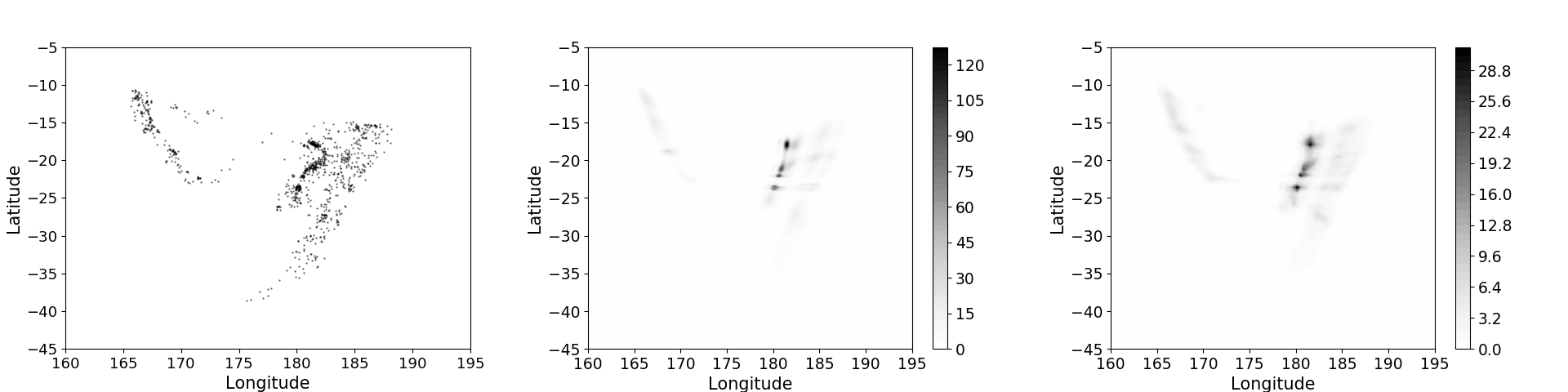
Figure 1. Left panel: Scatter plot of earthquake events with body-wave magnitude greater than 4.0 near Fiji since 1964. Middle panel: Estimated intensity function obtained using measure transport. Right panel: Estimated standard error of the intensity surface.
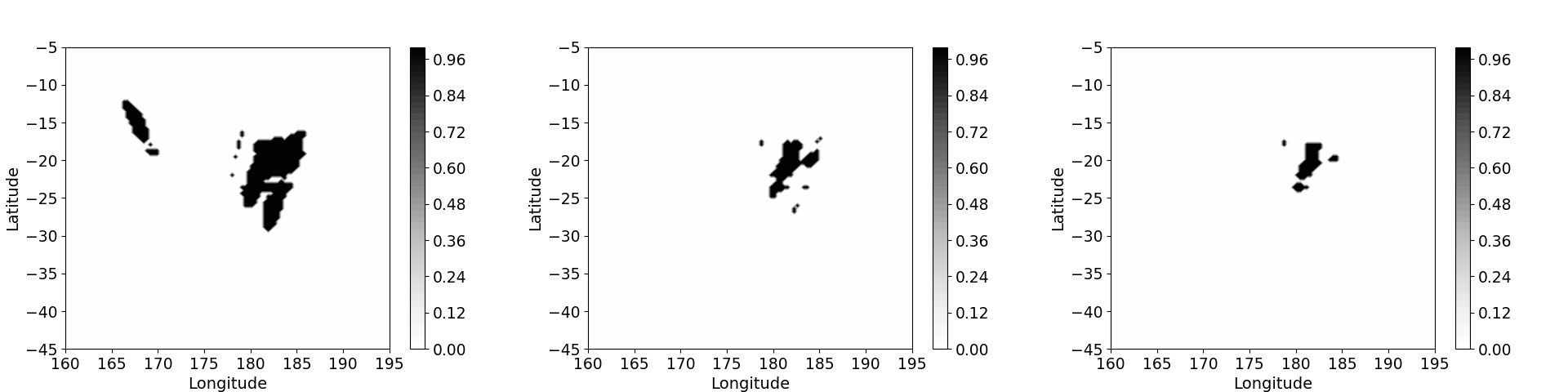
Figure 2. Left panel: Estimated exceedance probability \(P(\lambda(\cdot) > 1)\). Middle panel: Estimated exceedance probability \(P(\lambda(\cdot) > 5)\). Right panel: Estimated exceedance probability \(P(\lambda(\cdot) > 10)\).