Frozen percolation on the binary tree is nonendogenous

Definition of the model

To construct frozen percolation on a directed graph, we place a barrier on each directed edge. These barriers can be in three states:

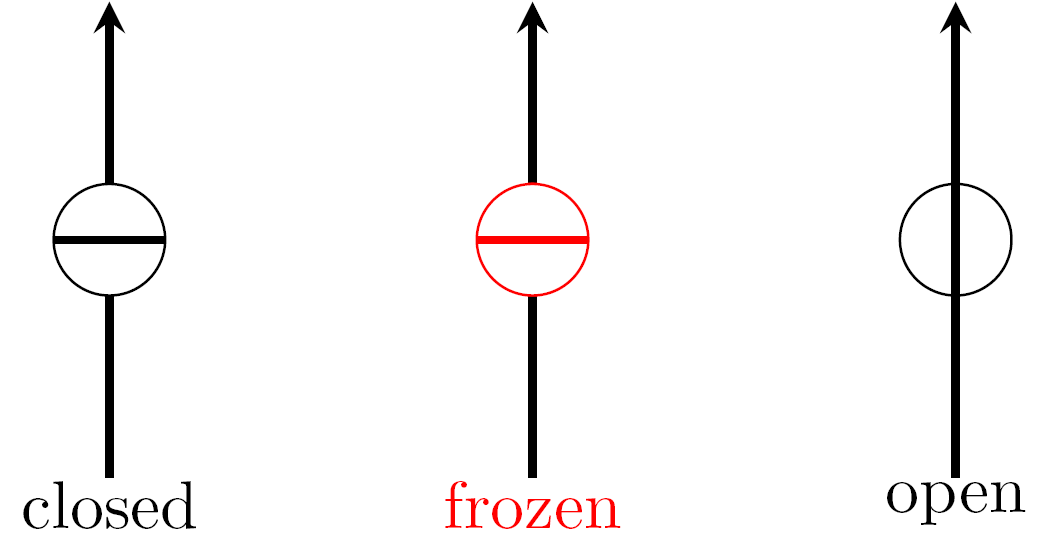
We assign i.i.d. Unif\([0,1]\) activation times \((\tau_\mathbf{i})_{\mathbf{i}\in{\mathbb B}}\) to the barriers \(\mathbf{i}\in{\mathbb B}\), and we fix a closed set \(\Xi\subset[0,1]\) of freezing times. The states of barriers evolve according to the following informal description:

• Initially, all barriers are closed.

• At its activation time, a barrier opens, provided it is not frozen.

• At each freezing time \(t\in\Xi\), all closed barriers that percolate are frozen.

Here, we say that a barrier percolates if there starts an infinite open path just above it:

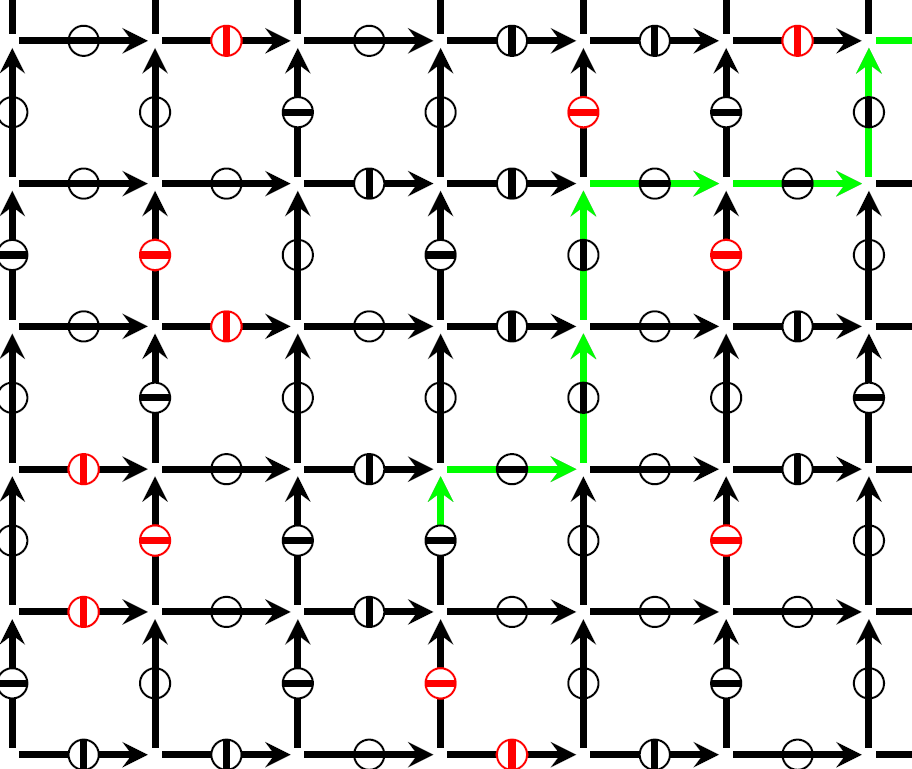
More formally, we set \[\begin{array}{r@{\,}c@{\,}l} \displaystyle{\mathbb A}_t&:=&\displaystyle\big\{\mathbf{i}\in{\mathbb B}:\tau_\mathbf{i}\leq t\big\},\\[5pt] \displaystyle{\mathbb F}&:=&\displaystyle\big\{\mathbf{i}\in{\mathbb B}:\mathbf{i}\mbox{ is frozen at the final time }1\big\}. \end{array}\] Then \({\mathbb A}_t\backslash{\mathbb F}\) is the set of barriers that are open at time \(t\). We write \(\mathbf{i}\overset{{{\mathbb A}_t\backslash{\mathbb F}}}{\longrightarrow}\infty\) if \(\mathbf{i}\) percolates at time \(t\). Then the Frozen Percolation Equation reads: \[{\mathbb F}=\big\{\mathbf{i}\in{\mathbb B}:\mathbf{i}\overset{{{\mathbb A}_t\backslash{\mathbb F}}}{\longrightarrow}\infty \mbox{ for some }t\in(0,\tau_\mathbf{i}]\cap\Xi\big\}\qquad({\rm FPE}).\] It is clear from our informal description that if \(\Xi\) is finite, then (FPE) has a solution \({\mathbb F}\), which is a.s. unique given the activation times \((\tau_\mathbf{i})_{\mathbf{i}\in{\mathbb B}}\). For general \(\Xi\) and general directed graphs, one can ask whether solutions exist and whether they are unique in distribution or perhaps even almost surely.

Frozen percolation can also be defined on undirected graphs. Just replace each undirected edge by two directed edges whose barriers are activated at the same time. The case \(\Xi=[0,1]\) is of special interest, since in this case clusters freeze as soon as they reach infinite size, which leads to self-organised criticality. For this reason, in the year 2000 David Aldous introduced frozen percolation (Aldous, 2000). He proved that the frozen percolation equation (FPE) has a solution on the undirected 3-regular tree, and that under natural assumptions this solution is unique in law. On the other hand, Itai Benjamini and Oded Schramm observed that (FPE) does not have a solution on the two-dimensional integer lattice. A sketch of their proof can be found in Section 3 of (van den Berg and Tóth, 2001).

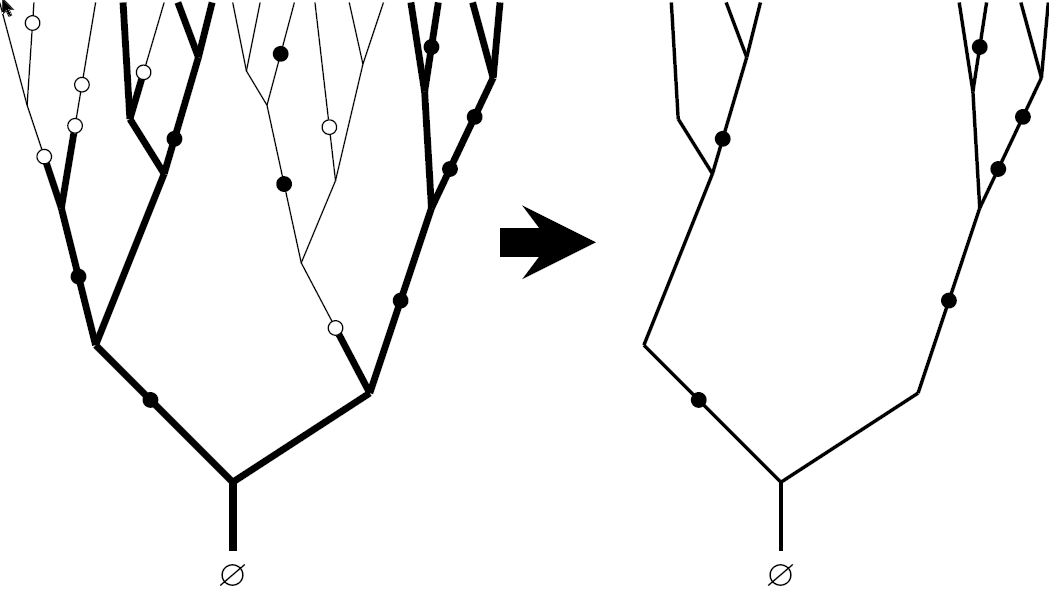
If from the directed binary tree \(T\), we remove a finite subtree \(U\) containing the root, then \(T\backslash U\) consists of finitely many disjoint subtrees \(T_1,\ldots,T_n\):

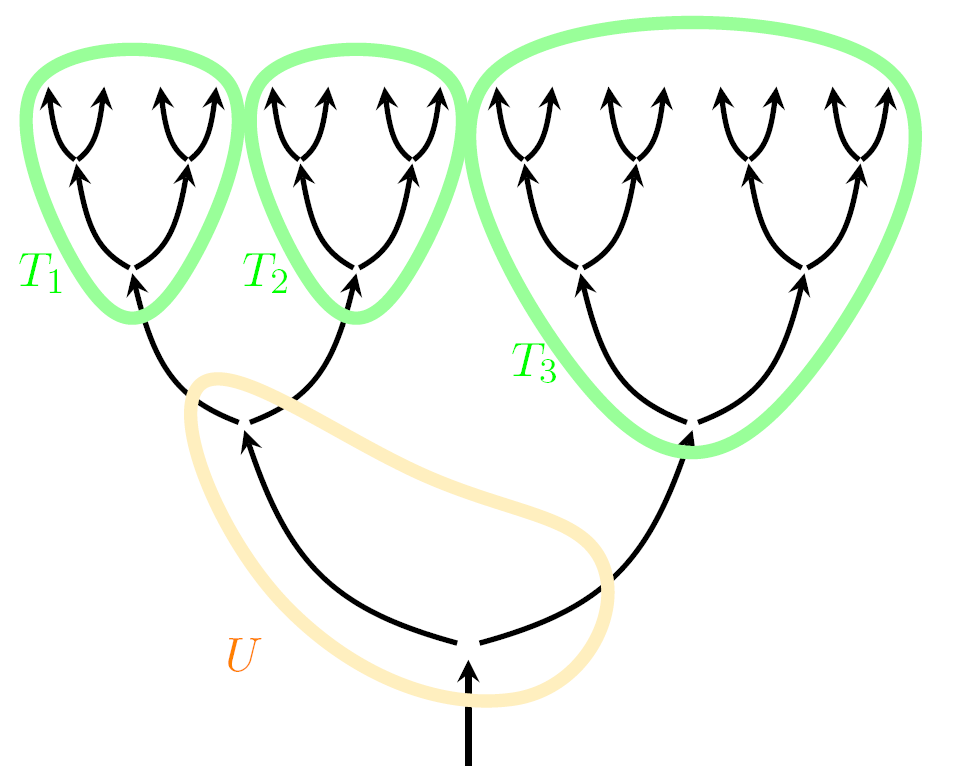
We say that a solution \({\mathbb F}\) satisfies the natural conditions if its restrictions to \(T_1,\ldots,T_n\) are i.i.d., equally distributed with the process on the whole tree \(T\), and independent of the activation times in \(U\). We label barriers in the obvious way and let \([\mathbf{i}]\) denote the vertex just below \(\mathbf{i}\):

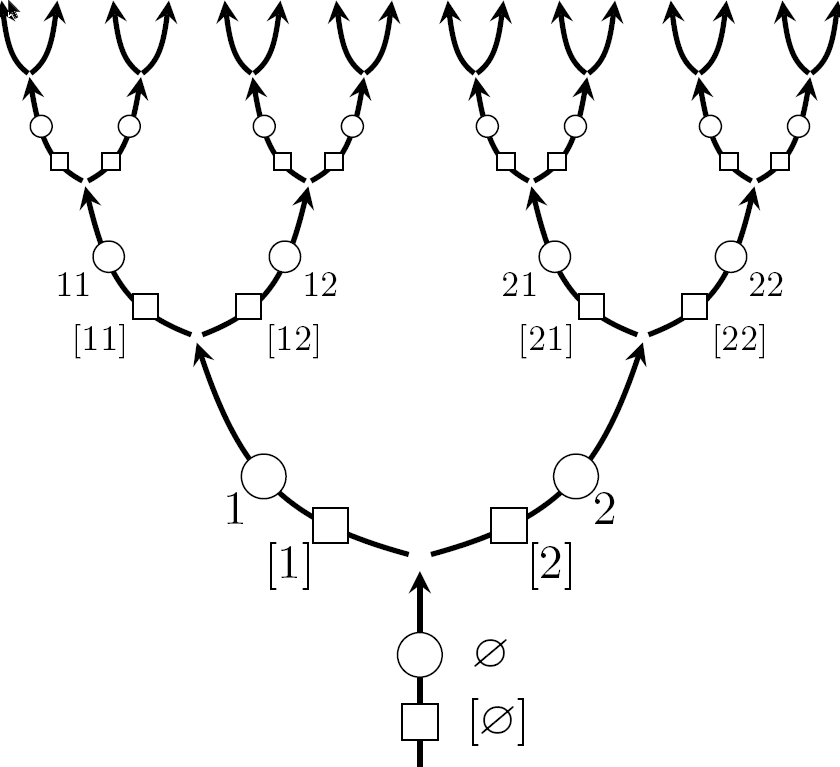
It is easy to see that the freezing time of the root \[Y_{[\varnothing]}:=\inf\big\{t\in\Xi:[\varnothing]\overset{{{\mathbb A}_t\backslash{\mathbb F}}}{\longrightarrow}\infty\big\}\] solves the Recursive Distributional Equation \[Y_{[\varnothing]}\stackrel{\scriptstyle{\rm d}}{=}\gamma(\tau_\varnothing,Y_{[1]},Y_{[2]}):=\left\{\begin{array}{ll} Y_{[1]}\wedge Y_{[2]}\quad&\mbox{if }\tau_\varnothing<Y_{[1]}\wedge Y_{[2]},\\[5pt] \infty\quad&\mbox{otherwise,} \end{array}\right.\quad({\rm RDE}),\] where, because the solution to (FPE) satisfies the natural conditions, \(Y_{[1]},Y_{[2]}\) are independent of each other and equally distributed with \(Y_{[\varnothing]}\), and \(\tau_\varnothing\) is an independent Unif\([0,1]\) distributed random variable.

The following theorem is a free formulation of of Theorem 1 and Lemma 5 from (Ráth, Swart and Szőke, 2021), which using Proposition 42 of (Ráth, Swart and Terpai, 2021) are translated into the present setting.

Theorem For each closed \(\Xi\subset[0,1]\), there exists a unique solution to (RDE) that yields a solution \({\mathbb F}\) to (FPE). In particular, for each closed \(\Xi\subset[0,1]\), (FPE) has a solution that satisfies the natural conditions, and the joint law of \(\big(\tau_\mathbf{i})_{\mathbf{i}\in{\mathbb B}},{\mathbb F}\big)\) is uniquely determined.

For the case \(\Xi=[0,1]\), this theorem was (basically) already proved in (Aldous, 2000) by Aldous, who showed that in this case the freezing time of the root has the law \[{\mathbb P}\big[Y_{[\varnothing]}>y\big]=1\wedge\frac{1}{2y}\qquad\big(y\in[0,1]\big),\] with \({\mathbb P}\big[Y_{[\varnothing]}=\infty\big]={\textstyle\frac{{1}}{{2}}}\).

To study almost sure uniqueness in this and related problems, David Aldous and Antar Bandyopadhyay (Aldous and Bandyopadhyay, 2005) developed a general theory of Recursive Tree Processes. In the general setting, almost sure uniqueness is called endogeny. Let \({\mathbb F},{\mathbb F}'\) be solutions to (FPE) that satisfy the natural conditions and are conditionally independent given \((\tau_\mathbf{i})_{\mathbf{i}\in{\mathbb B}}\). Then \((Y_{[\varnothing]},Y'_{[\varnothing]})\) solves the bivariate RDE \[(Y_{[\varnothing]},Y'_{[\varnothing]})\stackrel{\scriptstyle{\rm d}}{=} \big(\gamma(\tau_\varnothing,Y_{[1]},Y_{[2]}),\gamma(\tau_\varnothing,Y'_{[1]},Y'_{[2]})\big),\] where \(\gamma\) is the function from (RDE). In Theorem 11 of (Aldous and Bandyopadhyay, 2005), it is proved that \({\mathbb F}={\mathbb F}'\) a.s. if and only if each solution to the bivariate RDE with the right marginals is concentrated on the diagonal. After a failed proof of endogeny that turned out to contain an error (Bandyopadhyay, 2004), Antar Bandyopadhyay ran numerical calculations that strongly suggested almost sure uniqueness does not hold, but for 15 years nobody was able to prove this.

We discovered the problem becomes easier if we place a geometrically distributed number of barriers with mean one on each edge.

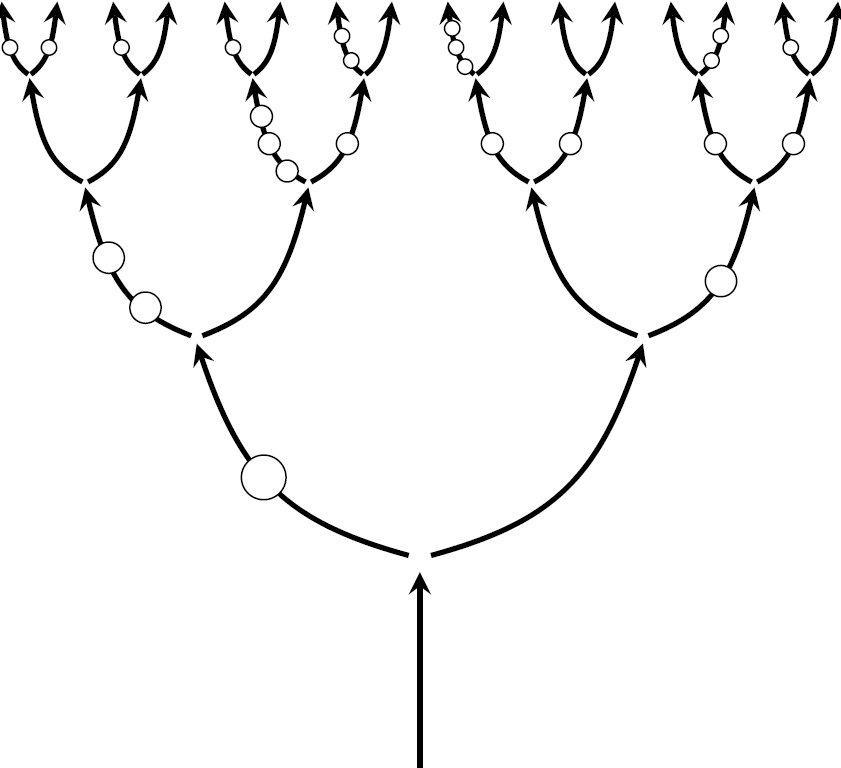
We call this the Marked Binary Branching Tree (MBBT). The MBBT naturally arises as the near-critical scaling limit of percolation on regular trees. Since it is itself a scaling limit, the MBBT has a natural scaling property. For fixed \(r\in[0,1]\), the pruned MBBT is obtained by removing all parts of the tree that do not percolate at time \(r\) even in the absence of freezing. For the MBBT, \({\mathbb P}\big[[\varnothing]\overset{{{\mathbb A}_r}}{\longrightarrow}\infty\big]=r\) and conditional on this event, the pruned tree is equally distributed with a scaled version of the original tree.

The bivariate RDE gives an integral equation for \[F(s,t):={\mathbb P}\big[Y_{[\varnothing]}\leq s,\ Y'_{[\varnothing]}\leq t\big].\] For the MBBT, scaling gives \(F(rs,rt)=rF(s,t)\) \((r,s,t\in[0,1])\). The bivariate RDE now reduces to an integral equation for a function of one variable, which is easier to solve than the original bivariate RDE for the binary tree. However, as demonstrated in Proposition 42 of (Ráth, Swart and Terpai, 2021), frozen percolation on the binary tree and on the MBBT can be translated into each other. The basic idea is that several barriers on one oriented edge can be replaced by a single effective barrier, whose activation time is the maximum of the activation times of the individual barriers. As a result, we were able to obtain Theorem 3 of (Ráth, Swart and Terpai, 2021), which says:

Theorem For frozen percolation on the binary tree with \(\Xi=[0,1]\), solutions to (FPE) are not almost surely unique.

In (Ráth, Swart and Szőke, 2021) we investigated almost sure uniqueness for frozen percolation on the MBBT for sets of freezing times of the form \(\Xi_\theta:=\{\theta^n:n\geq 0\}\) with \(0<\theta<1\). These sets behave well under scaling, so we were able to use the same techniques as in (Ráth, Swart and Terpai, 2021). To translate this back from the MBBT into the setting of the binary tree, one has to replace \(\Xi_\theta\) by its image under the map \(H(t):=1/(2-t)\) \((t\in[0,1])\). Theorem 9 of (Ráth, Swart and Szőke, 2021) says:

Theorem For frozen percolation on the MBBT and sets of freezing times of the form \(\Xi_\theta\), there exists a parameter \(\theta^\ast=0.636\ldots\) such that, if \({\mathbb F},{\mathbb F}'\) are solutions to (FPE) for \(\Xi_\theta\), that satisfy the natural conditions and are conditionally independent given \((\tau_\mathbf{i})_{\mathbf{i}\in{\mathbb B}}\), then \({\mathbb F}={\mathbb F}'\) a.s. if and only if \(\theta\leq\theta^\ast\).

We have an explicit formula for the parameter \(\theta^\ast\) (see Lemma 8 in (Ráth, Swart and Szőke, 2021)), which is rather complicated. The result shows that in general, one cannot hope to settle the question of almost sure uniqueness by “soft” arguments. Instead, any proof will always require some hard calculations.

A number of open problems remain, notably:

• We don’t know if distributional or almost sure uniqueness still hold if we drop the natural conditions.

• Almost sure (non-)uniqueness is open for \(n\)-regular directed trees with \(n\geq 3\) and for more general sets of freezing times \(\Xi\). The technical challenge is to replace perfect scale invariance in the proofs by approximate scale invariance near the critical point.

• Existence and/or uniqueness of solutions to (FPE) on more general graphs, including \({\mathbb Z}^d\) with \(d\geq 3\), is wide open.