Summary
We propose a higher order targeted maximum likelihood estimation (TMLE) that only relies on a sequentially and recursively defined set of data-adaptive fluctuations. Without the need to assume the often too stringent higher order pathwise differentiability, the method is practical for implementation and has the potential to be fully computerized.
Background
Targeted Maximum Likelihood Estimation (TMLE)
It has been particularly of interest for semiparametric theories and real world practices to make efficient and substitution-based estimation for target quantities that are functions of data distribution. TMLE (van der Laan and Rubin 2006; van der Laan and Rose 2011, 2018) provides a framework to construct such estimators and incorporates machine learning into efficient estimation and inference. Here we briefly review the regular first order TMLE.
Suppose that the true distribution \(P_0\) lies in a statistical model \(\mathcal{M}\). Start with an initial distribution estimator \(P_n^0\). Given pathwise differentiability of the target \(\Psi(P)\) at \(P\) with a canonical gradient \(D^{(1)}_P\), consider a least favorable path \(\{ \tilde P^{(1)}(P, \epsilon) \}\) through \(P\) at \(\epsilon=0\), where scores at \(\epsilon=0\) span the efficient influence curve (EIC) \(D_{P}^{(1)}\). Define the TMLE update by maximizing the likelihood along the path, that is, \(\epsilon_n^{(1)} = \mathrm{argmin}_\epsilon P_n L(\tilde P^{(1)}(P_n^0, \epsilon) )\), where \(L(P) = - \log p\). The resulted TMLE update is \(P_n^* = \tilde P_n^{(1)} (P_n^0) = \tilde P_n^{(1)} (P_n^0, \epsilon_n^{(1)})\).
Define \(R^{(1)}(P, P_0) = \Psi(P) - \Psi(P_0) + P_0 D_P^{(1)}\) as the exact remainder. Then the TMLE satisfies \(P_n D_{P_n^*}^{(1)}\approx 0\) and the following exact expansion \[ \Psi(P_n^*) - \Psi(P_0) = R^{(1)}(P_n^*, P_0) - P_0 D_{P_n^*}^{(1)} = (P_n - P_0) D_{P_0}^{(1)} + (P_n - P_0) (D_{P_n^*}^{(1)} - D_{P_0}^{(1)}) - P_n D^{(1)}_{P_n^*} + R^{(1)}(P_n^*, P_0). \] Asymptotic efficiency for \(P_n^*\) requires:
- \(\{D_{P}^{(1)}: P\in\mathcal{M}\}\) is a \(P_0\)-Donsker class (often satisfied, or skipped with sample splitting),
- Solving the equation \(P_n D^{(1)}_{P_n^*}=0\) exactly or to an \(o_P(n^{-1/2})\) term,
- \(R^{(1)}(P_n^*, P_0)\) being exactly zero or up to an \(o_P(n^{-1/2})\) term.
\(R^{(1)}(P, P_0)\) is often a second order difference in \(p\) and \(p_0\). For example, when it consists of cross products, doubly or multiply robustness may exist.
Highly Adaptive Lasso (HAL)
HAL (van der Laan 2015, 2017; Benkeser and van ver Laan 2016) is a nonparametric maximum likelihood estimator that converges in Kullback-Leibler dissimilarity at a minimal rate of \(n^{-2/3}(\log~n)^d\), even when the parameter space only assumes cadlag and finite variation norms. This generally bounds the exact remainder, and immediately makes the TMLE that uses HAL as an initial asymptotically efficient. However, in finite samples, the second order remainder can still dominate the sampling distribution.
Another important property of HAL is itself being a nonparametric MLE, so it can solve a large class of score equations to best approximates the desired score via increasing the \(L_1\)-norm of the HAL-MLE (called undersmoothing) (van der Laan, Benkeser, and Cai 2019a, 2019b).
Higher Order Fluctuations with HAL-MLE
Replace \(P_n^0\) in the first order TMLE by a TMLE \(\tilde P^{(2)}_n(P_n^0)\) of \(\Psi_n^{(1)}(P_0) = \Psi(\tilde P^{(1)}_n(P_0)) = \Psi(\tilde P^{(1)}(P_0, \epsilon_n^{(1)}(P_0)))\), which is a data-adaptive fluctuation of the original target parameter \(\Psi(P_0)\). Then the final update of a second order TMLE, \(\tilde P^{(1)}_n \tilde P^{(2)}_n(P_n^0)\), is just a first order TMLE that uses as the initial estimator a \(\tilde P^{(2)}(P_n^0)\) that is fully tailored for \(\Psi_n^{(1)}(P_0)\).
Figure 1: Left panel: regular TMLE. Right panel: second order TMLE. The horizontal axes represent the original target. The vertical axis represents the data-adaptive fluctuation. The second order TMLE searches for a better initial estimator for a regular TMLE.
Similarly if we iterate this process, and let \(\tilde P^{(k+1)}_n(P_n^0)\) be a regular TMLE tailored for a higher order fluctuation \(\Psi_n^{(k)}(P_0) = \Psi^{(k-1)}_n(\tilde P^{(k)}_n(P_0))=\Psi(\tilde P^{(1)}_n \tilde P^{(2)}_n\cdots \tilde P^{(k)}_n(P_n^0))\) for \(k=1, \ldots\), then the final update of a \(k+1\)-th order TMLE is \(\tilde P^{(1)}_n \tilde P^{(2)}_n\cdots \tilde P^{(k+1)}_n(P_n^0)\).
The second order TMLE relies on pathwise differentiability of \(\Psi_n^{(1)}\). However, \(\Psi_n^{(1)}(P) = \Psi(\tilde P^{(1)}_n(P)) = \Psi(\tilde P^{(1)}(P, \epsilon_n^{(1)}(P)))\)is smooth in \(P\) up till the dependence of \(\epsilon_n^{(1)}(P) = \mathrm{argmax}_\epsilon P_n \log \tilde p_n^{(1)}(p, \epsilon)\) on \(P\), because \(P_n\) is not absolutely continuous w.r.t. \(P\) for most \(P\) that can occur as an initial or a higher order TMLE-update. This calls for the use of smooth distribution estimators such as HAL-MLE \(\tilde{P}_n\) in replacement of the empirical \(P_n\), since \(d\tilde P_n/dP\) will exist for all \(P\) that can occur as an initial or higher order updates, which ensures pathwise differentiability of \(\Psi^{(1)}_n(P_0)\) and the existence of its canonical gradient \(D^{(2)}_{n, P}\).
In general, suppose that \(\{\tilde P^{(k)}_n(P, \epsilon)\}\) is a least favorable path through \(P\) at \(\epsilon=0\), whose scores at \(\epsilon=0\) span \(D^{(k)}_{n, P}\). And the update step is also replaced by optimizing the \(\tilde P_n\)-regularized loss, that is, \(\epsilon_n^{(k)} = \mathrm{argmin}_\epsilon \tilde P_n L(\tilde P^{(k)}(P_n^0, \epsilon) )\), which solves \(\tilde P_n D^{(k)}_{n, P}=0\) at \(P = \tilde P^{(k)}_n(P_n^0)= \tilde P^{(k)}_n(P_n^0, \epsilon_n^{(k)})\).
A \(k+1\)-th order TMLE by its design searches for a better initial estimator given the \(k\)-th order TMLE. Specifically, the \(k+1\)-th order TMLE moves in the same direction as the steepest descent algorithm for minimizing the \(k\)-th exact total remainder that is the discrepancy between \(\Psi(\tilde P^{(1)}_n \tilde P^{(2)}_n\cdots \tilde P^{(k)}_n(P)) - \Psi(\tilde P^{(1)}_n \tilde P^{(2)}_n\cdots \tilde P^{(k)}_n(P_0))\) and \(\tilde{P}_n D^{(k)}_{n, P_0}\). Moreover, compared to an oracle steepest descent algorithm, TMLE stops the moment the log-likelihood is not improving anymore, which corresponds exactly to when the TMLE cannot know in what direction a steepest descent algorithm would go. This avoids potential overfitting and ensures a local minimum in close neighborhood of the desired (but unknown) minimum \(P_0\).
Exact Expansions of Higher Order TMLE
Denote the \(k\)-th exact remainder as the exact remainder of \(\tilde P^{(k)}_n(P)\) for the fluctuation \(\Psi^{(k-1)}(P_0) = \Psi(\tilde P_n^{(1)}\cdots\tilde P_n^{(k-1)}(P_0))\):
\[\begin{align*} R^{(k)}_n(\tilde P^{(k)}_n(P), P_0) = & \Psi^{(k-1)}(\tilde P^{(k)}_n(P)) - \Psi^{(k-1)}(P_0) + P_0 D^{(k)}_{n, \tilde P^{(k)}_n(P)} \\ = & \Psi(\tilde P^{(1)}\cdots\tilde P^{(k)}_n(P)) - \Psi(\tilde P^{(1)}\cdots\tilde P^{(k-1)}(P_0)) + P_0 D^{(k)}_{n, \tilde P^{(k)}_n(P)}. \end{align*}\]
Then we have the exact expansion for the \(k\)-th order TMLE,
\[\begin{align*} \Psi(\tilde P^{(1)}_n\cdots\tilde P^{(k)}_n(P)) - \Psi(P_0) = & \sum_{j=1}^{k-1} (P_n-P_0)D^{(j)}_{n, \tilde P^{(j)}_n(P_0)} + R^{(j)}_n(\tilde P_n^{(j)}(P_0), P_0) \\ & + (P_n-P_0)D^{(k)}_{n, \tilde P^{(k)}_n}(P_n^0) + R^{(k)}_n(\tilde P_n^{(k)}(P_n^0), P_0) \\ & - \sum_{j=1}^{k-1} P_n D^{(j)}_{n, \tilde P^{(j)}_n(P_0)} - P_n D^{(k)}_{n, \tilde P^{(k)}_n(P_n^0)}, \end{align*}\]
which still holds if we replace \(P_n\) with \(\tilde P_n\). This can be further derived as
\[\begin{align*} \Psi(\tilde P^{(1)}\cdots\tilde P^{(k)}_n(P)) - \Psi(P_0) =&\sum_{j=1}^{k}\left\{ (\tilde{P}_n-P_0)D^{(j)}_{n,\tilde{P}_n^{(j)}(P_0)}+R_n^{(j)}(\tilde{P}_n^{(j)}(P_0),P_0)\right\} \\ %&&+(P_n-P_0)D^{(k)}_{n,P_n^{(k)}(P_0)}\\ & +R_n^{(k)}(\tilde{P}_n^{(k)}(P_n^0),\tilde{P}_n)-R_n^{(k)}(\tilde{P}_n^{(k)}(P_0),\tilde{P}_n)\\ &-\sum_{j=1}^{k}\tilde{P}_n D^{(j)}_{n,\tilde{P}_n^{(j)}(P_0)}.\end{align*}\]
The followings can be shown:
- \((\tilde{P}_n-P_0)D^{(j)}_{n,\tilde{P}_n^{(j)}(P_0)}, j=1, \dots, k,\) are generalized \(j\)-th order difference in \(P_0\) and \(\tilde P_n\), which resemble the performance of higher order \(U\)-statistics;
- \(R_n^{(j)}(\tilde{P}_n^{(j)}(P_0),P_0) = O_P(n^{-1})\) given \((\tilde P_n - P_n) D_{n, P_0}^{(j)} = O_P(n^{-1/2})\), which can be achieved by undersmothing HAL;
- \(R_n^{(k)}(\tilde{P}_n^{(k)}(P),\tilde P_n)\) is a generalized \(k+1\)-th order difference in \(P\) and \(\tilde P_n\), and hence \(R_n^{(k)}(\tilde{P}_n^{(k)}(P_n^0),\tilde P_n) - R_n^{(k)}(\tilde{P}_n^{(k)}(P_0),\tilde P_n)=o_P(n^{-1/2})\) so long as \(\lVert \tilde p_n - p_0 \rVert = o_P(n^{1/2(k+1)})\) and \(\lVert p_n^0 - p_0 \rVert = o_P(n^{1/2(k+1)})\);
- The last term can be exactly \(0\) by defining \(\epsilon_n^{(j)}(P)\) as a solution of the corresponding efficient score equation \(\tilde P_n D^{(j)}_{n, \tilde P^{(j)}_n(P, \epsilon)}=0\).
Higher Order Inference
For the sake of statistical inference, we will need that \((\tilde P_n - P_n)D^{(1)}_{\tilde P_n^{(1)}(P_0)} = o_P(n^{-1/2})\), and probably even \((\tilde P_n - P_n)D^{(j)}_{\tilde P_n^{(j)}(P_0)} = o_P(n^{-1/2})\) for \(j = 2, \dots, k\). It can be shown that this essentially comes down to controlling \((\tilde P_n - P_n) D^{(1)}_{P_0}\), which again can be achieved by undersmoothing HAL.
Let \[ \bar D_n^k = \sum_{j=1}^k D^{(j)}_{n, \tilde P^{(j)}_n\cdots\tilde P^{(k)}_n(P_n^0)} \] which is an estimate of the influence curve \(\bar D_{n, P_0}^k = \sum_{j=1}^k D^{(j)}_{n, \tilde P^{(j)}_n(P_0)}\). Note that for \(j>1\) the terms are higher order differences, so that \(\bar D_n^k\) will converge to the efficient influence curve \(D^{(1)}_{P_0}\).
Let \[ \sigma_n^2 = \frac{1}{n}\sum_{i=1}^n \bar D_n^k(O_i)^2 \] be the sample variance of this estimated influence curve. A corresponding 0.95 confidence interval is given by \[ \Psi(P^{(1)}_n\cdots\tilde P^{(k)}_n(P_n^0)) \pm 1.96 \sigma_n/n^{1/2}. \]
Simulation
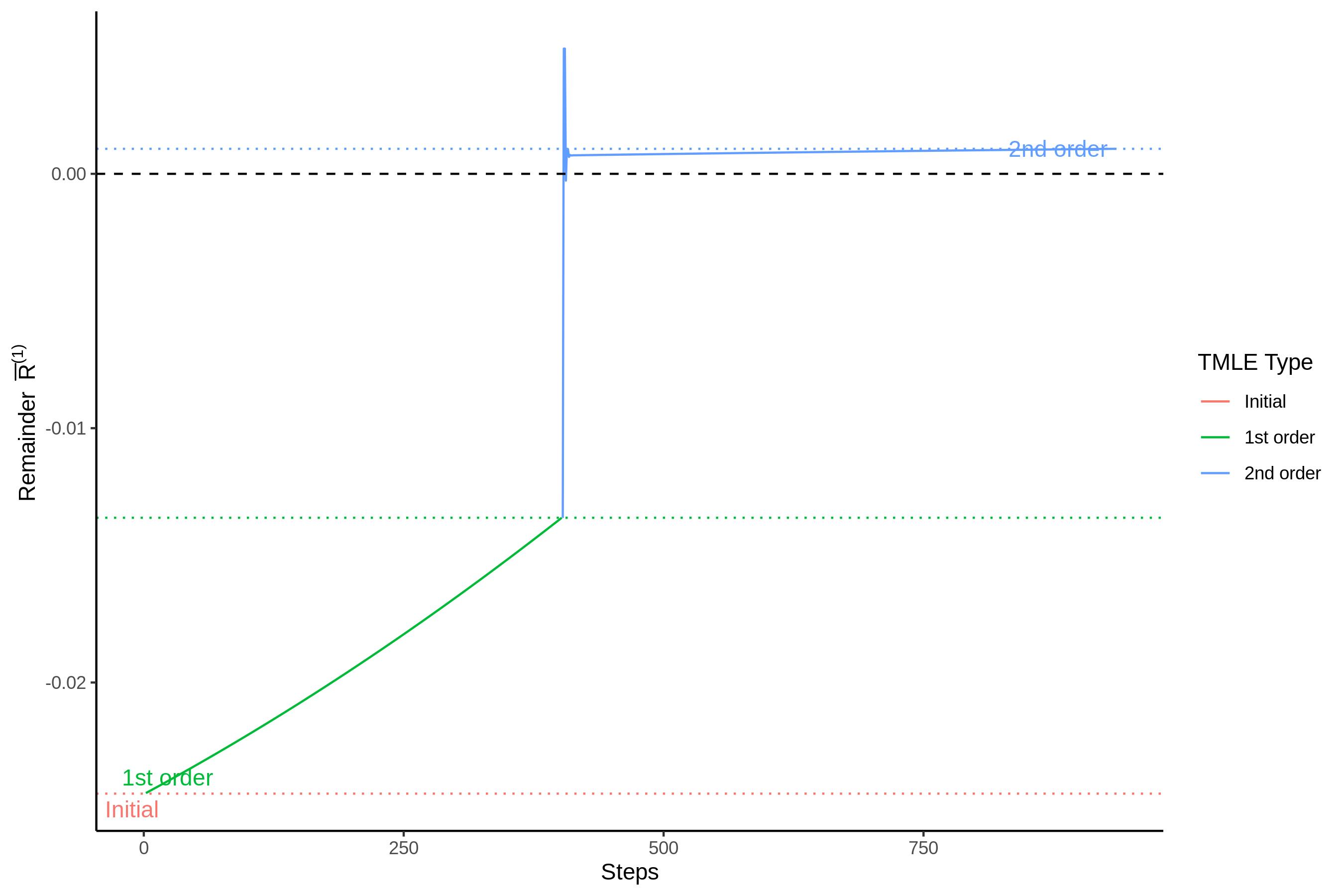
The first example demonstrates the impact of second order TMLE steps during a process of estimating the average density. The exact total remainder \(\bar R^{(1)}(\tilde P_n^{(1)}(P), P_0)\) of first order TMLE is controlled due to the second order updates \(P = P_n^0 \mapsto \tilde P_n^{(2)}(P_n^0)\).
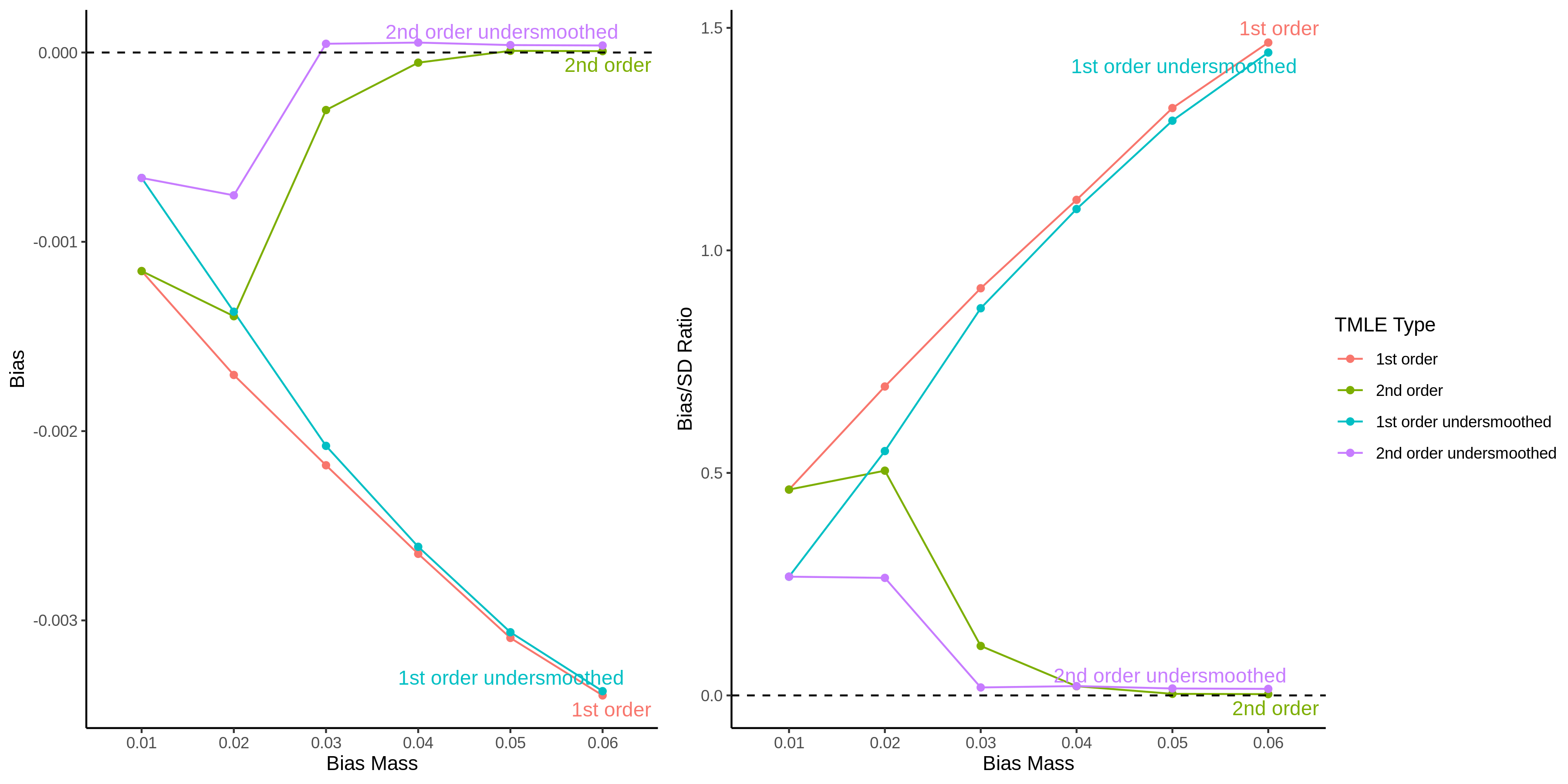
Below it plots the simulated bias and bias/SD ratio at \(n=500\) when we increase the bias in the initial estimator \(P_n^0\) by adding a bias mass to each of the support points of the empirical pmf. Second order TMLE provides improved accuracy in both estimation and inference over first order TMLE following likelihood guidance.
Lastly, we show an example of estimating average treatment effects (ATEs) while the initial estimator for propensity scores is \(n^{-1/4}\)-consistent while that for outcome models is not. The first order TMLE should have \(n^{1/2}\)-scaled bias that increases with \(n\) while the second order TMLE has a \(n^{1/2}\)-bias that should be constant in \(n\). The table below shows that the second order TMLE has a negligible bias and thereby still provides valid inference.
| n | bias 1-st | bias 2-nd | se 1-st | se 2-nd | mse 1-st | mse 2-nd |
|---|---|---|---|---|---|---|
| 400 | -0.720 | 0.078 | 0.815 | 1.175 | 1.087 | 1.178 |
| 750 | -0.996 | 0.029 | 0.800 | 1.102 | 1.278 | 1.102 |
| 1000 | -1.258 | -0.062 | 0.786 | 1.066 | 1.483 | 1.068 |
| 1200 | -1.345 | 0.022 | 0.809 | 1.028 | 1.570 | 1.028 |
| 1600 | -1.549 | -0.019 | 0.818 | 1.055 | 1.752 | 1.055 |
| 2500 | -2.066 | -0.094 | 0.819 | 0.999 | 2.222 | 1.003 |
Discussions
Although HAL-MLE-based fluctuations are fundamental to higher order TMLE, the update steps in practice can be based on empirical losses. Note that the \(j-1\)-th fluctuation \(\Psi(\tilde P_n^{(1)}\cdots\tilde P_n^{(j-1)}(P_0))\), \(j = 0, \dots, k-1\), is nothing but a pathwise differentiable parameter with a known canonical gradient, \(D^{(j)}_{n, P}\). For jointly targeting this sequence of \(k\) parameters, one can solve the empirical \(P_n\)-regularized efficient score equations (where the scores still involve HAL-MLEs). As we showed in the technical report, this preserves the exact expansion and even leads to an improved undersmoothing term, and therefore is the recommended implementation. At \(k=1\), this exactly coincides with the regular first order TMLE.
Figure 2: Jointly consider the sequence of data-adaptive fluctuations.
An important next step is the (automated) computation of the first and higher order canonical gradients with least squares regression or symmetric matrix inversion (van der Laan, Wang, and van der Laan 2021), thereby opening up the computation of higher order TMLEs with standard machinery, avoiding delicate analytics needed to determine closed forms.