Correlations and negative bias
We assume that you are quite familiar with the following problem. Consider a data set where the information is expressed in percentages or proportions. An example are household expenditures, given as average amounts (in Euros) the households are spending on food, housing, transportation, etc. Since the expenditures would not be comparable among countries with very different economic level, it makes sense to express the data as proportions (or percentages) of the single categories on the total expenditures. Now one can be interested in relationships between the different variables (expenditure categories), and the common tools for this task would be to use the Pearson or Spearman correlation coefficient to determine the strength of the associations. However, is this appropriate to compute correlations from percentages (or proportions, or any other constrained data), or more generally, from data carrying relative information? Denote the underlying variables, expressed in proportions or percentages, by \(x_1,\ldots,x_D\). When computing correlations, we must count with a negative bias of the covariance, which leads to relations like \[\mathrm{cov}(x_1,x_2)+\mathrm{cov}(x_1,x_3)+\ldots+\mathrm{cov}(x_1,x_D)=-\mathrm{var}(x_1).\] Consequently, the correlation coefficients cannot vary freely between \(-1\) and \(1\); they are forced towards negative values and thus do not produce reliable and interpretable results.
Initial choice: variation matrix
The way to obtain reasonable correlations with percentage data is to consider ratios, or even mathematically easier, log-ratios as the source information. Log-ratios do not change when the data are rescaled, thus the sum of components (100 for percentages) is even irrelevant. In our household expenditure data set we could thus even work with the raw data, expressed in Euros, and the results of the analysis would be the same as for the normalized data. The scale invariant data are called compositional in this context. A natural way to assess strength of relationship between components of percentage (compositional) data is thus to think in terms of their proportionality. This leads to the so called variation matrix, which is defined as \[\mathbf{T}=\left(\mathrm{var}\left(\ln\frac{x_i}{x_j}\right)\right)_{i,j=1}^D.\] If the components are proportional, the respective element of the variation matrix is zero, and vice versa. Thus, bigger values of the variation matrix refer to deviations from proportionality. Here, var is denotes the variance, and practically one can use classical or robust variance estimation, where the latter is preferable in presence of outliers. The variation matrix is thus definitely a reasonable choice to express relationship between the variables, however, it cannot be interpreted in terms of correlations, as possible negative relationships between the components are not captured.
Correlations with (weighted) symmetric pivot coordinates
We can see that relating the original components has its clear limitations. A possible alternative could be to consider relative information carried by the original components of a given composition, information contained in log-ratios to other components. The first choice is to aggregate these logratios which leads, say for components \(x_1\) and \(x_2\), to the following variables (we refer to symmetric pivot coordinates): \[\begin{eqnarray} z_1^s&=&C\left(\frac{\sqrt{D-2}}{\sqrt{D-2}+\sqrt{D}}\ln\frac{x_1}{x_2}+\ln\frac{x_1}{x_3}+\ldots+\ln\frac{x_1}{x_D}\right),\\ z_2^s&=&C\left(\frac{\sqrt{D-2}}{\sqrt{D-2}+\sqrt{D}}\ln\frac{x_2}{x_1}+\ln\frac{x_2}{x_3}+\ldots+\ln\frac{x_2}{x_D}\right), \end{eqnarray}\] with a normalizing positive constant \(C\). The first logratios in both variables are downscaled in order to remove a possible negative bias (from a geometrical perspective, we are talking about orthonormality of the resulting variables/coordinates); interestingly, \(\sqrt{D-2}/(\sqrt{D-2}+\sqrt{D})\rightarrow 1/2\) as \(D\rightarrow\infty\). Even more, the effect of pairwise logratios which are aggregated into \(z_1^s\) and \(z_2^s\) can be weighted, e.g., according to their proportionality to \(x_1\) and \(x_2\), respectively, by using the inverse values of the respective elements of \(\mathbf{T}\). This guarantees that components not related to \(x_1\) and \(x_2\) have a limited impact to the construction of both symmetric pivot coordinates.
Now, standard (classical or robust) correlation coefficients between \(z_1^s\) and \(z_2^s\) can be computed to estimate the relationship between \(x_1\) and \(x_2\) in the composition. Its interpretation follows directly the construction of symmetric pivot coordinates. This means that the original components are replaced by their dominance over “averaged” contributions of the other components (ev. appropriately weighted) – a quite natural interpretation for data carrying relative information. Moreover, the correlation can be considered in both the positive and negative sense without any danger of the negative bias. We should be only aware that each correlation coefficient is coming from a set of coordinates which are constructed specifically for the given couple of components, so the resulting “correlation matrix” should not be simply treated in the multivariate sense.
Relative structure of household expenditures
Let us come back to the initial example where the interest was in the relative structure of household expenditures, reported for several countries of the European Union.
Such a data set is contained as expendituresEU in the library robCompositions. With a
proportional representation of the expenditures the wealth status of countries is
suppressed and the focus is on the relative correlation structure. In order to suppress the influence of outlying observations, the Spearman correlation coefficients between
the components are computed and the result is plotted in the heatmap below.
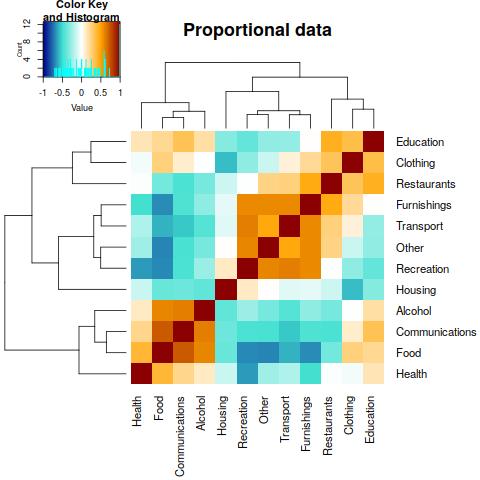
There are some strongly related groups of components visible, like Foodstuff, Alcohol and Communications, which could be considered as those belonging to “basic” expenditures, and there is also another related group of components which could be connected rather to wealth of households (Recreation, Furnishing, Transport and Other). On the other hand, there are also some strongly negatively correlated couples of components, like Food with Recreation, Other and Furnishings, respectively, or Recreation and Health. The question is which of these negative correlation coefficients is a consequence of the negative bias, and which indeed reflects strong negative relationship between the relative household expenditures.
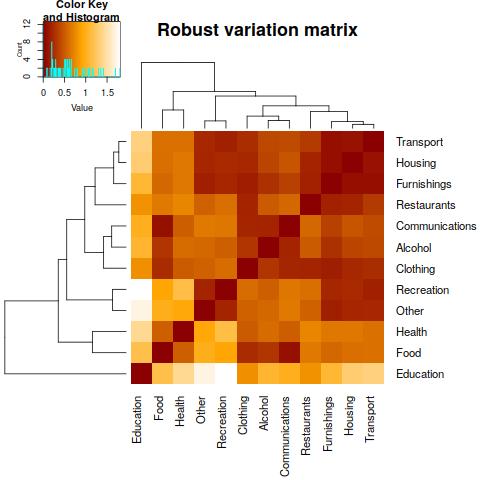
As the next step we want to see whether these relationships can be observed also in the (robust) variation matrix, working with log-ratios instead of the original components. Indeed, the proportionality holds definitely for the first group of components (Foodstuff, Alcohol and Communications), however, proportionality of supplementary expenditures is now structured differently (see, e.g., a strong relationship between the components Recreation and Other). In any case, any “negative proportionality” cannot be derived from the variation matrix.
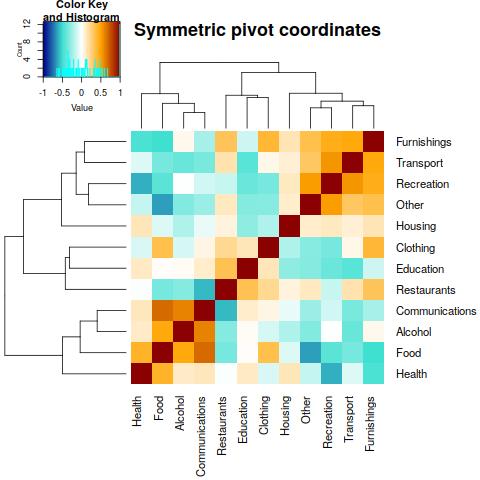
Therefore, we turn to symmetric pivot coordinates; they can be computed, similarly as the variation matrix, using the robCompositions package:
library(robCompositions)
data(expendituresEU)
D <- ncol(expendituresEU)
Rs <- matrix(NA,nrow=D,ncol=D)
rownames(Rs) <- colnames(expendituresEU)
colnames(Rs) <- colnames(expendituresEU)
for(i in 1:D){
for(j in 1:D){
Z <- pivotCoord(expendituresEU[,c(i,j, (1:D)[-c(i,j)])],method="symm")
Rs[i,j] <- cor(Z[,1:2],method="spearman")[1,2]
}
}
round(Rs,2)## Food Alcohol Clothing Housing Furnishings Health Transport
## Food 1.00 0.58 0.31 -0.06 -0.55 0.44 -0.50
## Alcohol 0.58 1.00 -0.02 -0.09 -0.22 0.19 -0.35
## Clothing 0.31 -0.02 1.00 -0.16 0.24 -0.07 0.08
## Housing -0.06 -0.09 -0.16 1.00 0.24 0.15 0.29
## Furnishings -0.55 -0.22 0.24 0.24 1.00 -0.54 0.68
## Health 0.44 0.19 -0.07 0.15 -0.54 1.00 -0.29
## Transport -0.50 -0.35 0.08 0.29 0.68 -0.29 1.00
## Communications 0.72 0.66 0.03 -0.08 -0.51 0.32 -0.47
## Recreation -0.44 -0.03 -0.17 0.36 0.73 -0.51 0.78
## Education 0.16 0.09 0.16 -0.32 -0.24 0.13 -0.44
## Restaurants -0.44 -0.42 0.18 0.13 0.39 -0.08 0.28
## Other -0.64 -0.28 -0.16 0.32 0.68 -0.27 0.67
## Communications Recreation Education Restaurants Other
## Food 0.72 -0.44 0.16 -0.44 -0.64
## Alcohol 0.66 -0.03 0.09 -0.42 -0.28
## Clothing 0.03 -0.17 0.16 0.18 -0.16
## Housing -0.08 0.36 -0.32 0.13 0.32
## Furnishings -0.51 0.73 -0.24 0.39 0.68
## Health 0.32 -0.51 0.13 -0.08 -0.27
## Transport -0.47 0.78 -0.44 0.28 0.67
## Communications 1.00 -0.24 0.15 -0.61 -0.35
## Recreation -0.24 1.00 -0.44 0.11 0.75
## Education 0.15 -0.44 1.00 0.33 -0.42
## Restaurants -0.61 0.11 0.33 1.00 0.21
## Other -0.35 0.75 -0.42 0.21 1.00Now the correlations are not computed from the original components and we have to refer to their dominance over averaged contributions of the other components instead, but the negative bias of correlations is eliminated now. Indeed, when looking at the heatmap, the main clusters of strongly positively correlated components remain unchanged. However, more substantial changes can be observed for negative correlations. From those mentioned previously only that one between Food and Other (in the symmetric pivot coordinates sense) remained. Nevertheless, we should be aware that for the computation of correlations we simply aggregated all log-ratios of the couple with the remaining components, and there are clearly those which could strongly influence the resulting symmetric pivot coordinates, although they are not related to any of components of interest. This is definitely the case of Education, which is not proportional to the vast majority of components (see heatmap of the variation matrix), and whose influence should thus be rather suppressed.
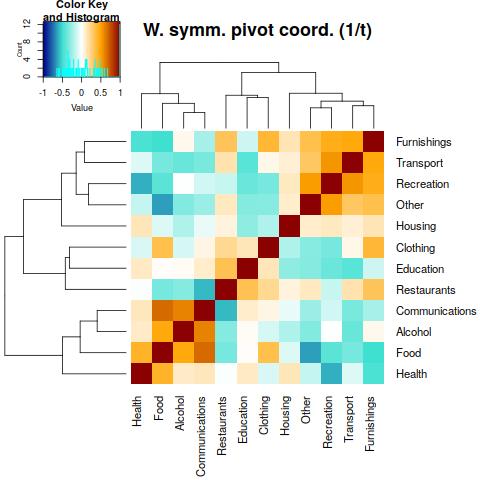
This can be done by using weighted symmetric pivot coordinates, the grouping of positively correlated components is now suprisingly even more similar to the case of the initial proportional data. Of course, by considering a different interpretation of the “components” in both cases! However, now we are free again from any possible negative bias of correlations. The “tuned” symmetric pivot coordinates reveal three negative relationships, those between Recreation and Health, Food and Other, and also Restaurants and Communications. All of them have a quite intuitive interpretation and support the take-home message that (weighted) symmetric pivot coordinates are a reasonable alternative to correlations of proportional or percentage data.
This article is based on
Filzmoser, P. Hron, K. and Templ, M. (2018) Applied Compositional Data Analysis. With Worked Examples in R. Springer Series in Statistics. Springer, Cham, Switzerland, 2018, ISBN: 978-3-319-96422-5.
Kynčlová, P., Hron, K., Filzmoser, P. (2017) Correlation between compositional parts based on symmetric balances. Mathematical Geosciences, 49 (6), 777-796.
Hron, K., Engle, M., Filzmoser, P., Fišerová, E. (2021) Weighted symmetric pivot coordinates for compositional data with geochemical applications. Mathematical Geosciences, https://doi.org/10.1007/s11004-020-09862-5

