A New Approach to Treatment Selection to Benefit Patient Outcomes in Clinical Trials

¹Introduction: Selecting Best Treatment

The question of selecting the “best” amongst different choices is a common problem in our lives. In clinical trials, our main field research, the question usually translates to “Out of a number of alternative treatments, which one treats the patients best?”.

A traditional approach to answer this question is to randomise equal numbers of patients to new treatments and the current method of treatment used in practice, called standard of care (SoC). Subsequently you compare the groups when the outcome for all patients is known. This is known as Equal Allocation, depicted in Figure 1 (A), and results in a high accuracy, meaning that if there is truly a difference between treatments, there is a high chance to find it.

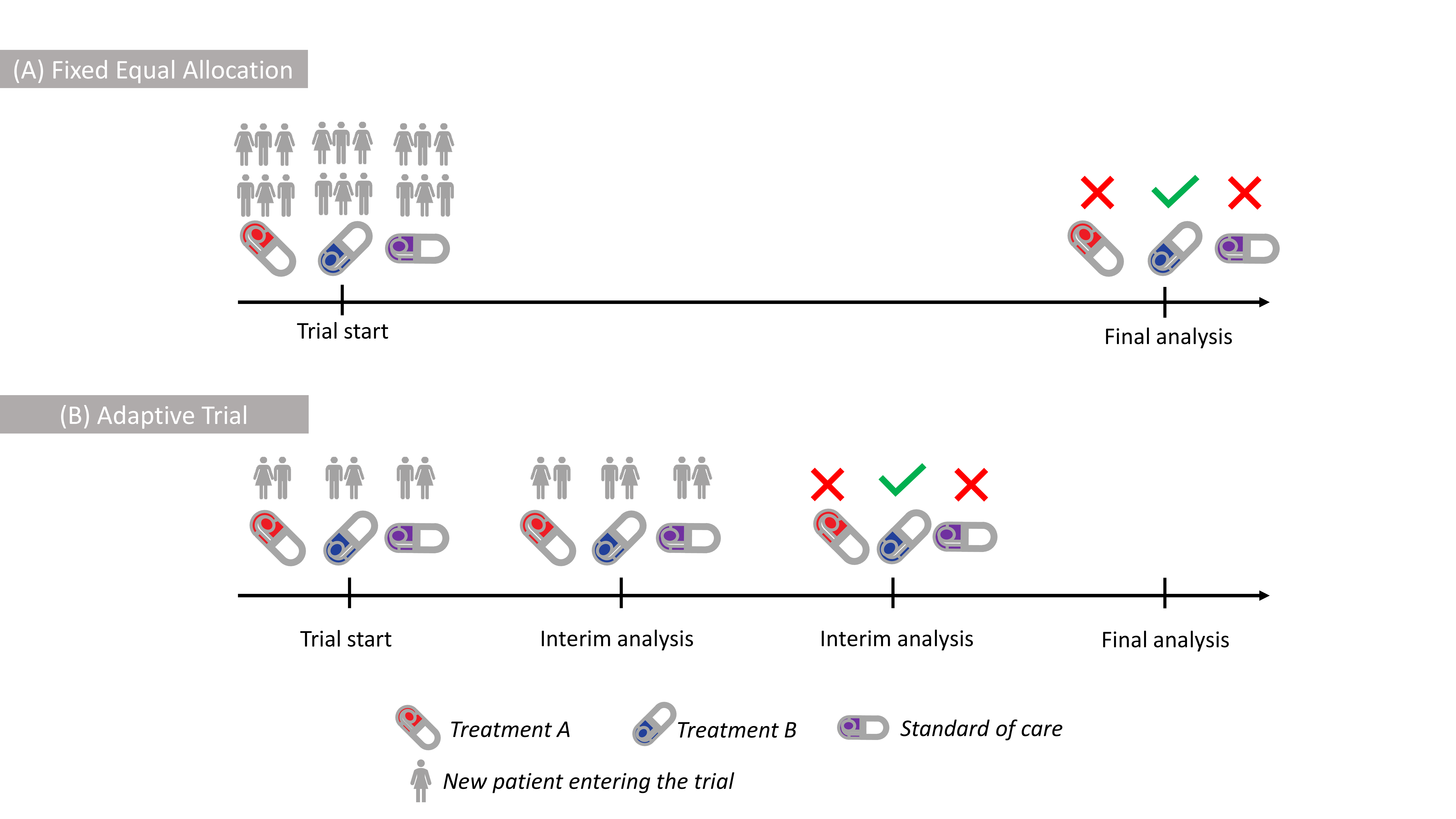Figure 1: Illustration of (A) Fixed Equal Allocation with all patients being allocated at the trial start, (B) Adaptive Trial with patients enrolled in stages with the Blue Treatment being selected at the 2nd interim.

However, since there typically is only one best treatment, many patients in such trials would be assigned to sub-optimal treatments.

Can we do better than that and offer more benefit to the patients participating in trials?

An alternative approach is to look at data as they accumulate and adapt whether which treatments should continue further in the trial. For example, if a treatment is found to be worse than the current SoC it would be stopped. Such studies are known as Adaptive Trials, depicted in Figure 1 (B). However, even if ineffective treatments are dropped earlier, the patient will usually have the same chance of receiving any of the remaining treatments. Essentially, this is due to the assumption that new information about each treatment is equally valuable to us. This, however, might not be the case in many situations as we are typically more interested in better performing treatments.

New Criterion to Select Treatments

The amount of uncertainty about a treatment is usually measured by an information measure, among which the Fisher Information and Shannon’s entropy are the most famous in Statistics. These measures do not depend on the value of the outcomes themselves, or simply, on the context of these outcomes.

The “context” of the trial can be included into the information measures directly using a weight function that gives more value to the points of specific interest and, essentially, reflects that information about treatments which are more effective is more valuable.

In our recent work, we have proposed to use the difference of the standard and weighted (Shannon) information measures (also known as the information gain) as a criterion to drive treatment selection in Response-Adaptive Trials, depicted in Figure 2.

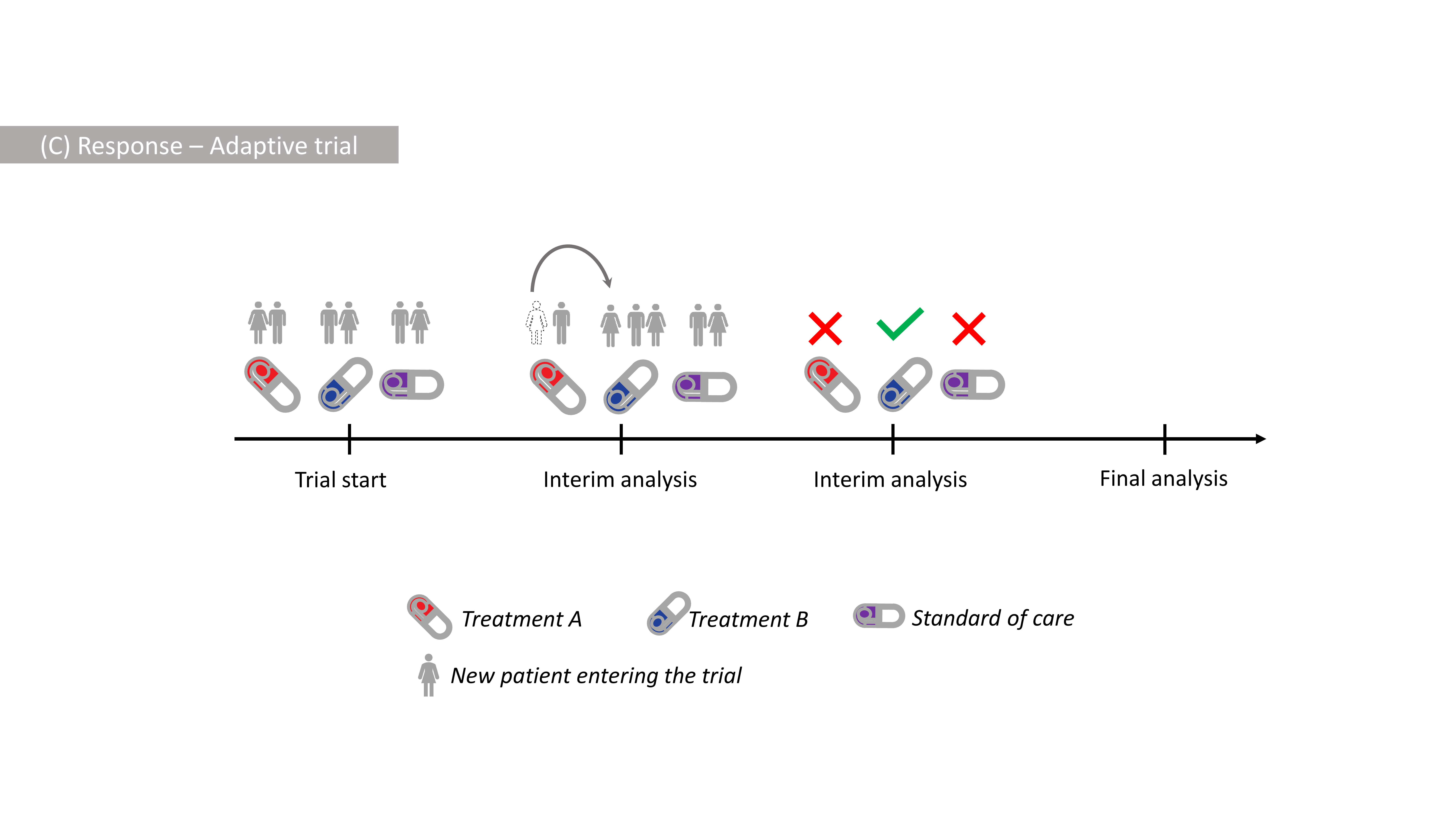Figure 2: Illustration of Response-Adaptive Design with more patients receiving a better Blue Treatment after the 1st interim, and the Blue Treatment being selected at the 2nd interim.

The new criterion

• leads to collecting more information about more effective treatments and hence results in more ethical allocation of patients (compared to the Equal Allocation);

• accounts for the uncertainty around treatments and allows for a reliable comparison between the selected treatment and standard of care.

Example of Potential Benefit

To demonstrate the benefit from our proposal, consider a hypothetical clinical trial. Assume that there are 3 new treatments, A, B, and C to be compared against the SoC in a trial of 423 patients enrolled one after the other. Assume that 30% of patients respond given treatments A and B and SoC, and 50% of patients respond given treatment C. We would like

1. to have sufficient information to claim that treatment C is indeed the best;

2. to assign as many patients to treatment C as possible.

These two goals are competing against each other as patients need to be assigned to other treatments to make sure C is best, but the new approach allows to balance these goals. Under a specific choice, our proposed criterion for the treatment $j$ is $$\Delta_j = \frac{\left(\hat{p}_j-1 \right)^2}{2 \hat{p}_j (1-\hat{p}_j)} \times n_j^{0.3}$$ which characterises how far the fraction of recovered patients given treatment $j$, $\hat{p}_j$, is from the best possible probability of recovery, $p=1$, (numerator), taking into account the uncertainty around this estimate (denominator), and the number of patients, $n_j$, assigned to this treatment (multiplicator). The criterion is updated after the outcome for previous patient is known.

The first goal will be measured via the chance to reliably claim that treatment C is better than SoC while the second goal is measured by the average number of patients that have responded.

We compare two approaches on how such trial can be conducted

• Randomising patients equally to A, B, C and SoC with probability 1/4 each;

• Randomising patients proportionally to the new criterion $\Delta_j$;

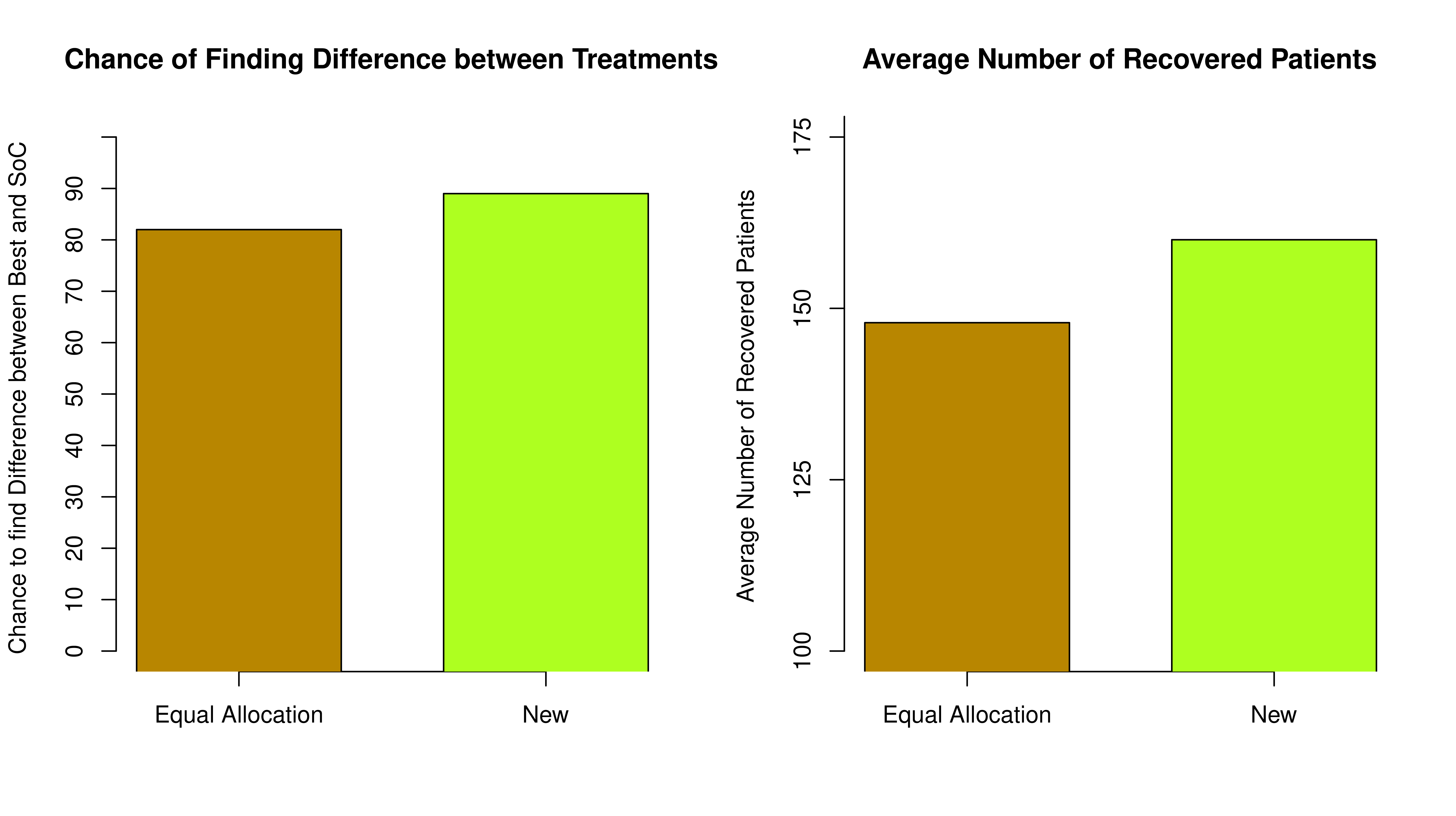
From Figure 3 we can see that the Equal Randomisation approach results in just over 80% chance of reliably claiming that the treatment C is indeed better than SoC while our proposed approach results in nearly 90% due to more patients being assigned to the best treatment - so a more reliable conclusion can be made.

Furthermore, under the Equal Allocation, the average number of patients who have responded in the trial is smaller. An additional 18 patients would have responded if the new randomised approach is used.

Overall, the new approach can be more ethical as it results in more patients benefiting from participating in the trial while not compromising the chances of finding the difference between the treatments.

While clinical trials have been the main motivation for this research, the design can be applied to a wide range of problems of similar nature, for example, online advertising, portfolio design, queuing and communication networks, etc.

This post is based on:

Mozgunov, P. and Jaki, T. (2020), An information theoretic approach for selecting arms in clinical trials. J. R. Stat. Soc. B. doi:10.1111/rssb.12391