As the COVID-19 pandemic spread across the world at the beginning of 2020, statistically modeling its development became of big interest. The main focus of this work was to analyze the spread of the disease and its main characteristics for Slovenia using publicly available COVID-19 data. Our work takes a Bayesian semiparametric approach using which we estimate some of the main measures of interest for the pandemic (e.g. the reproduction number $R_{t}$) and give accurate forecasts of important indicators for the following days. The provided methodology gives a flexible approach for modeling the COVID-19 pandemic which can be further adapted given the epidemiological and data specifics for a certain country.

The new coronavirus SARS-CoV-2 has quickly spread all around the world greatly impacting all aspects of our lives. One of the key reasons for its rapid spread is the high reproduction number of infection, $R_{t}$. The $R_{t}$ value represents the average number of people that an individual infects during their infection period, whereby $t$ represents time. $R_{t}$ is susceptible to change, for example, due to non-pharmaceutical governmental interventions (e.g. school closure or complete lockdown). When $R_{t} < 1$, the incidence of new cases reduces, but when $R_{t} > 1$, it increases until the epidemic reaches its peak; after that, the incidence of new cases starts to reduce due to (at least temporal) herd immunity. The estimates of the basic (i.e. initial) reproduction number, $R_{0}$, for SARS-CoV-2 vary substantially, depending on the method of estimation, and stand at about 3. Such a high basic reproduction number leads to a steep exponential increase in the number of cases which, in turn, causes a rapid increase in the number of people in need of hospitalization and intensive care unit (ICU). Due to the limited capacities of the healthcare system, this can lead to a situation where it is impossible to provide suitable care to all patients in need. Thus, it is of crucial importance for policymakers to estimate $R_{t}$ by which the spread of the epidemic could be monitored. But for better understanding of the epidemiological characteristics, we are also interested in estimating further measures, e.g. the infection fatality rate (i.e. the proportion of deaths among infected individuals), the proportion of asymptomatic cases and forecasting the number of hospitalized patients and patients in the ICUs.

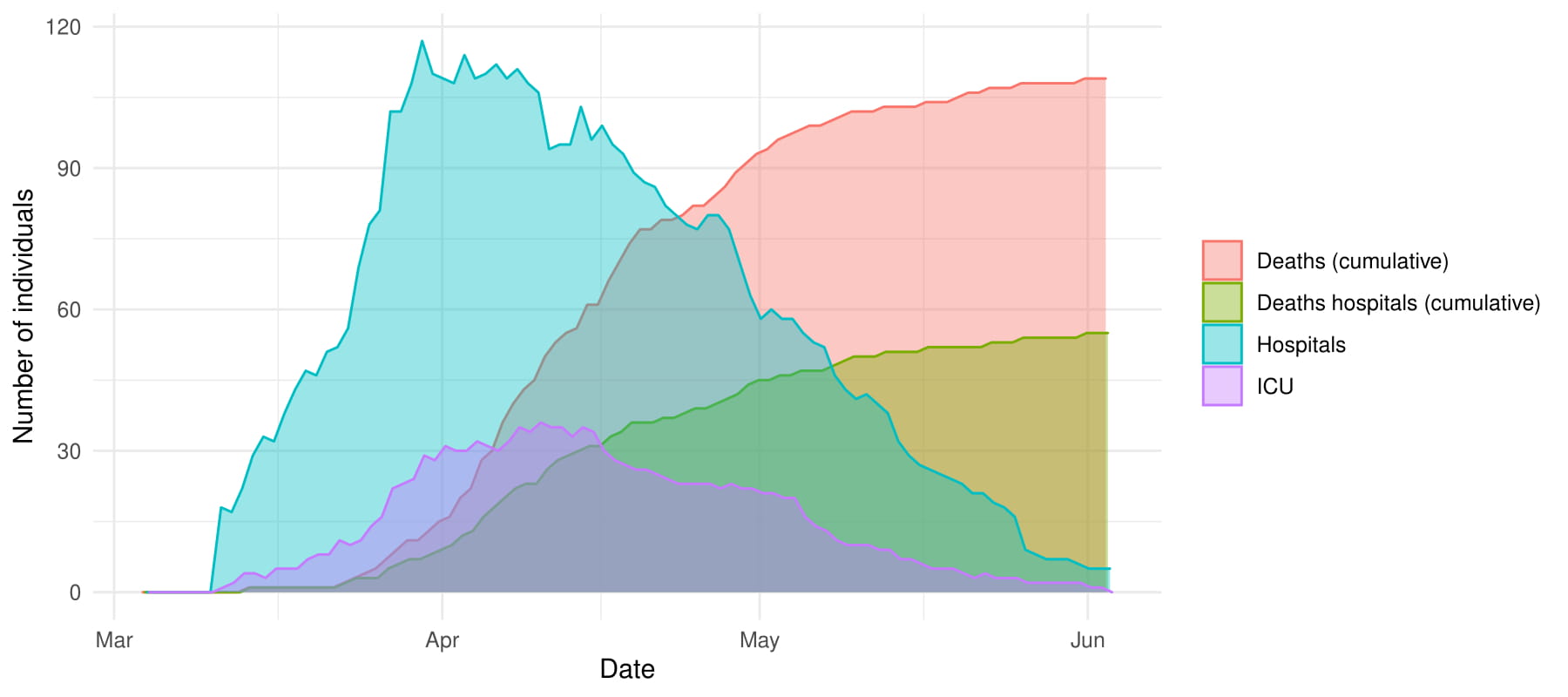
Figure 1 Number of patients treated in hospitals and ICUs on a given date, cumulative number of deaths and cumulative number of deaths occurring in hospitals in Slovenia, March 4–June 3, 2020.

In the current COVID-19 pandemic many governments have adopted non-pharmaceutical interventions (NPIs) to control the spread of the epidemic in their countries. Many models are available for forecasting the COVID-19 pandemic with adopted NPIs, e.g. SIR-like (Susceptible–Infected–Recovered-like) compartmental models or network-based models, which mimic the behavior of all individuals in the population. Models based on Bayesian inference were also introduced as an alternative to these two approaches. Here, simple stochastic models which describe the key features of epidemic spread are formulated and then actual data are used to estimate the parameters of the model, thus allowing the analysis to be driven by data and using less assumptions and/or fixed parameters. Furthermore, the final estimates are equipped with statistically sound intervals of uncertainty.

At the beginning of the epidemic, Flaxman et al. studied the influence of NPIs relying on Bayesian inference, using data for 11 European countries. Although this work gave very promising results it did have some flaws that would be problematic for the case of Slovenia. The Flaxman model is solely driven by the amount of deaths, which for a country of size like Slovenia does not provide a lot of information. Thus it was of main interest to include additional available data sources for Slovenia to make outputs as accurate as possible. In our work we have additionally included the following data sources: confirmed number of cases, number of patients in hospitals and in intensive care, and number of patients admitted to and released from hospitals and ICUs. Some of this information is presented on Figure 1 with data up to and including June 3, 2020 (all results presented in this report are up until this date).

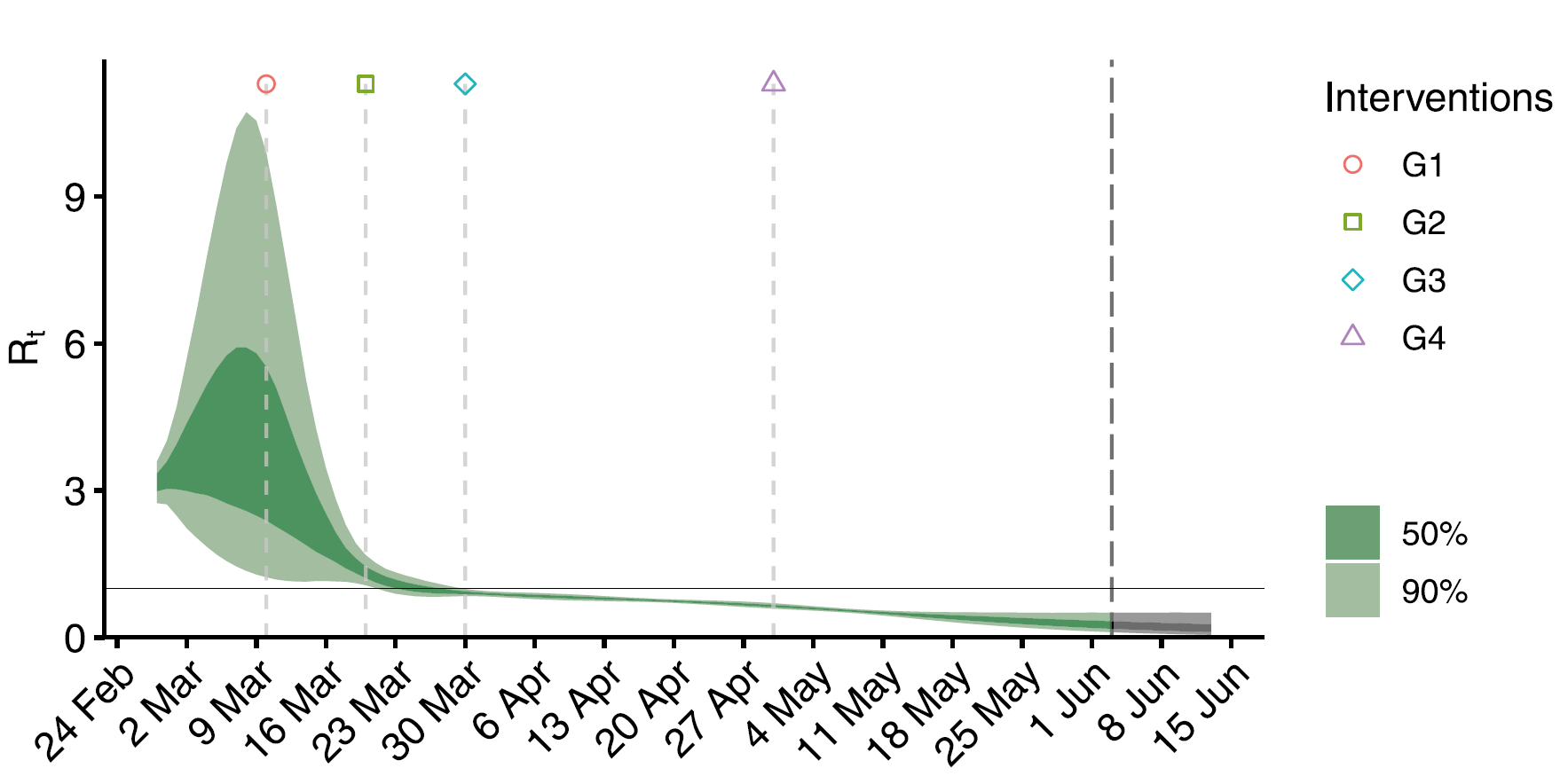
Figure 2 Estimated 50% and 90% credible intervals for the reproduction number $R_{t}$ for Slovenia March 4–June 3, 2020, with marked days of NPIs: G1 (March 10, 2020; public events banned), G2 (March 20, 2020; implementation of complete lock-down), G3 (March 30, 2020; prohibition of movement outside of the municipality of residence), G4 (April 30, 2020; some restrictions start to relax)

In our work we have proposed an elaborated semiparametric modeling framework based on a Bayesian approach, that greatly extends and modifies the Flaxman model. Apart from allowing for multiple data sources in the model, we also relax the assumption that the reproduction number $R_{t}$ is piece-wise constant; rather, we model it as time-varying. The extended model also allows us to report other measures, such as the proportion of unidentified cases, infection fatality rate, the proportion of cumulatively infected people and the number of patients in different disease progression states in time. In this report, we do not provide exact definitions and technical details for the proposed model, but full details are available in the articles cited below.

We first report on the estimated reproduction number $R_{t}$ for Slovenia, which is shown on Figure 2. The reproduction number has increased from 3.17 in the beginning (90% CI [2.74–3.59]) to 3.92 (90% CI [1.56–9.68]) until the adoption of measures to control the epidemic, after which the effective $R_{t}$ started to decrease reaching its lowest value of 0.17 (90% CI [0.05–0.51]) at the end of the study period. Based on these results it can be concluded that the adopted NPIs in Slovenia were effective in slowing down the spread of the epidemic which eventually resulted in the end of the first wave of the pandemic.

Based on the estimates of the number of infected individuals and estimated number of deaths, we estimate that throughout the study period the infection fatality rate (IFR) was 1.56% (90% CI [0.94–2.21]%) which at first seems large since other studies tend to report it around 0.5%–1%. This can be explained by noting that during the first wave of Slovene epidemic, the virus transmitted largely among older people inside retirement homes who are at much higher risk of dying due to COVID-19. Up to May 4, around 80% of all deaths occurred among people from retirement homes and all deaths outside the hospitals were in retirement homes. Excluding the estimated number of deaths occurring outside the hospitals yields a much smaller IFR of 0.80% (90% CI [0.48–1.26]%) thus more closely agreeing with other studies. It is of importance therefore to prevent the spread of the virus among the elderly.

Based on the proposed model we have also estimated the proportion of cumulatively infected people (i.e. the so-called attack rate) of 0.350% (90% credible interval (CI): [0.245–0.573]%) of the Slovene population suggesting that Slovenia had one of the smallest attack rates in Europe. It is also estimated that throughout the study period the proportion of unidentified cases, which can account for asymptomatic cases, was equal to 88% (90% CI [83-93]%). Unidentified cases can to some extent be attributed to asymptomatic or mild symptomatic cases but could also reflect the testing strategy of a country. Asymptomatic cases can transmit the virus causing difficulties in the control of the epidemic. Other studies have estimated that 40% to 45% of those infected with SARS-CoV-2 remain asymptomatic with large differences between the studies (from 17.9% to 87.9%). A large estimate for Slovenia might be a consequence of the fact that people with mild symptoms during the first wave were instructed to self-isolate and were in large majority not tested for SARS-CoV-2.

We can thus conclude that the proposed methodology can give us many measures that we are interested in when analyzing the development of the COVID-19 epidemic. The proposed framework is flexible and can be further extended to more data sources (if available) or other countries/regions (thus allowing for comparison between them). Additionally, with the predictions given for the number of patients in hospitals and intensive care units, policymakers could make data-driven decisions to potentially avoid overloading the capacities of the healthcare system.

Although in this report we have focused on an earlier study period (up to June 3, 2020), estimates (and forecasts) for Slovenia have been provided for later times and they are still daily updated and shown on the following link. As a strong second wave of the COVID-19 pandemic is expected throughout Europe in autumn 2020, we believe that the proposed methodology can be used for monitoring the pandemic. New epidemiological findings for COVID-19 are still arriving and some of them have yet to be included in the model. Thus, further improvements are still possible and we would like to examine them in the near future.

This article is based on

Manevski, D., Ružić Gorenjec N., Kejžar N., Blagus, R. (2020). Modeling COVID-19 pandemic using Bayesian analysis with application to Slovene data. Mathematical Biosciences, 329, article 108466

Manevski, D., Pohar Perme M., Blagus R. (2020). Estimation of the reproductive number and the outbreak size of SARS-CoV-2 in Slovenia. Slovenian Medical Journal, 89, pp. 1-12

About the authors

Damjan Manevski, Faculty of Medicine, University of Ljubljana, Slovenia, damjan.manevski@mf.uni-lj.si

assist. dr. Nina Ružić Gorenjec, Faculty of Medicine, University of Ljubljana, Slovenia, nina.ruzic@mf.uni-lj.si

doc. dr. Nataša Kejžar, Faculty of Medicine, University of Ljubljana, Slovenia, natasa.kejzar@mf.uni-lj.si

doc. dr. Rok Blagus, Faculty of Medicine, University of Ljubljana, Slovenia, rok.blagus@mf.uni-lj.si

prof. dr. Maja Pohar Perme, Faculty of Medicine, University of Ljubljana, Slovenia, maja.pohar@mf.uni-lj.si